Exploration into Optimal State Estimation with Event-triggered Communication
Paper and Code
Sep 15, 2023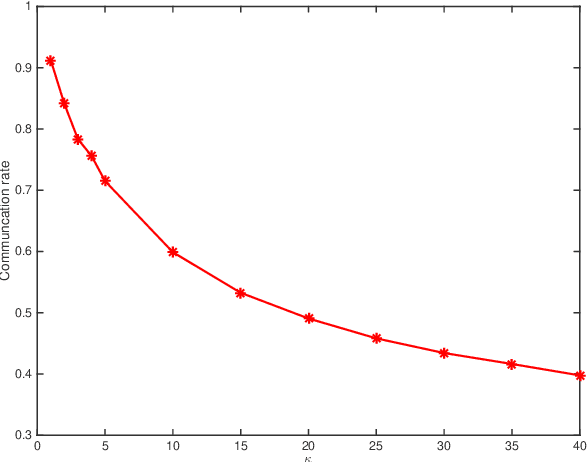
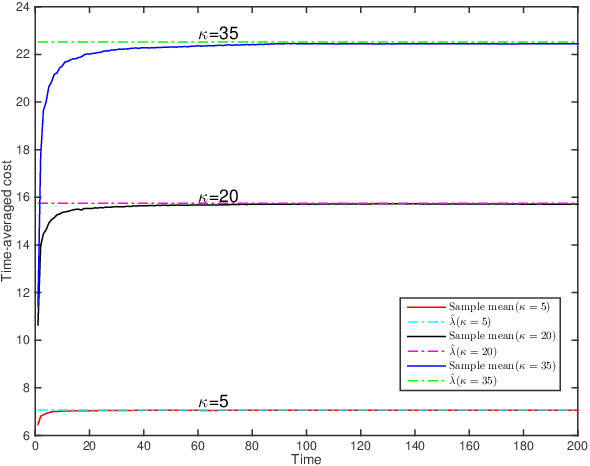
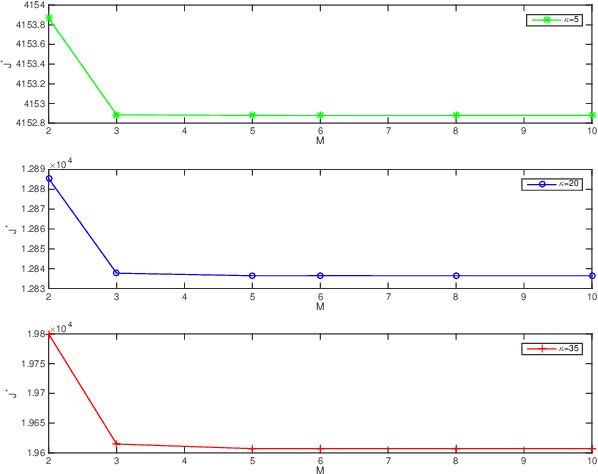
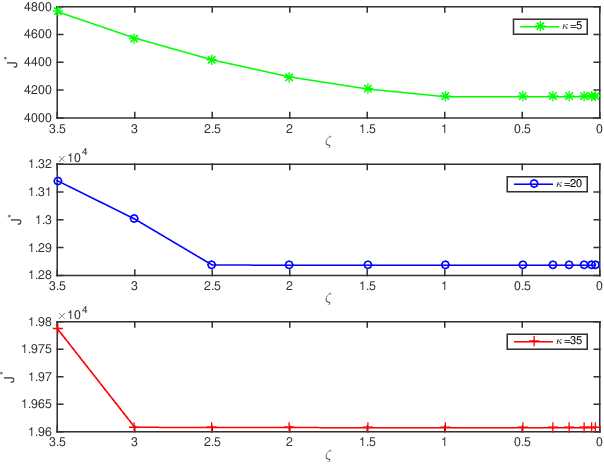
This paper deals with the problem of remote estimation of the state of a discrete-time stochastic linear system observed by a sensor with computational capacity to calculate local estimates. We design an event-triggered communication (ETC) scheme and a remote state estimator to optimally calibrate the tradeoff between system performance and limited communication resources. The novel communication scheme is the time-varying thresholding version for the cumulative innovation-driven communication scheme in [1], and its transmission probability is given. We derive the corresponding remote minimum mean square error (MMSE) estimator and present a tight upper bound for its MSE matrices. We also show that by employing a couple of weak assumptions, the optimality problem becomes (asymptotically) exact and can be addressed in an Markov Decision Process (MDP) framework, which delivers optimal policy and cost in an algorithmic procedure. The simulation results illustrate the effectiveness of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge