Guidance Trajectory Mathematical Modeling

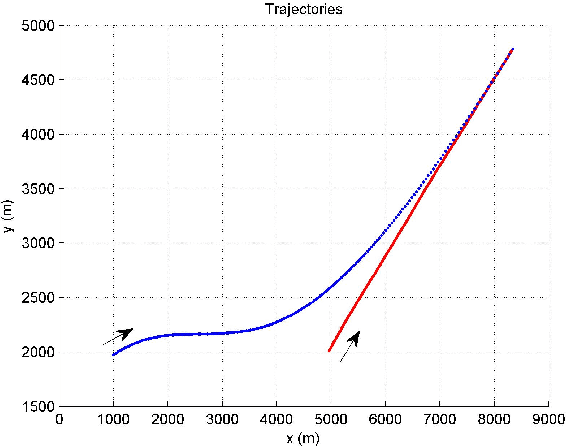
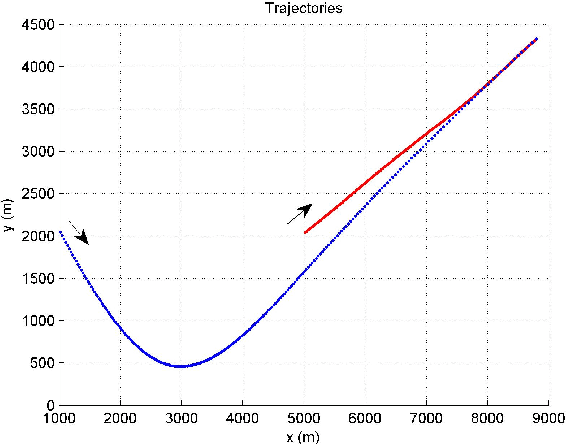
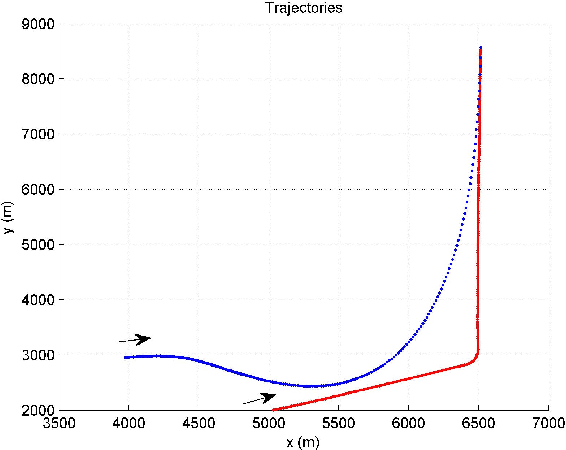
A trajectory of a destination-directed moving object (e.g. an aircraft from an origin airport to a destination airport) has three main components: an origin, a destination, and motion in between. We call such a trajectory that end up at the destination \textit{destination-directed trajectory (DDT)}. A class of conditionally Markov (CM) sequences (called CM$_\text{L}$) has the following main components: a joint density of two endpoints and a Markov-like evolution law. A CM$_\text{L}$ dynamic model can describe the evolution of a DDT but not of a guided object chasing a moving guide. The trajectory of a guided object is called a \textit{guided trajectory (GT)}. Inspired by a CM$_\text{L}$ model, this paper proposes a model for a GT with a moving guide. The proposed model reduces to a CM$_\text{L}$ model if the guide is not moving. We also study filtering and trajectory prediction based on the proposed model. Simulation results are presented.