Quantum One-class Classification With a Distance-based Classifier

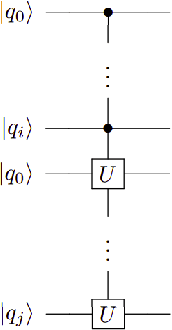
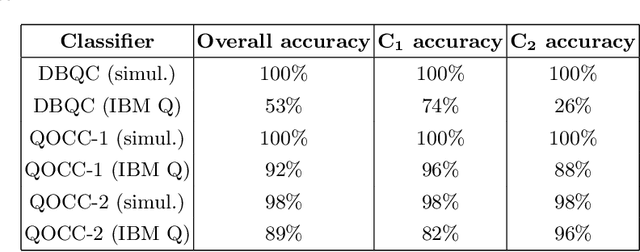
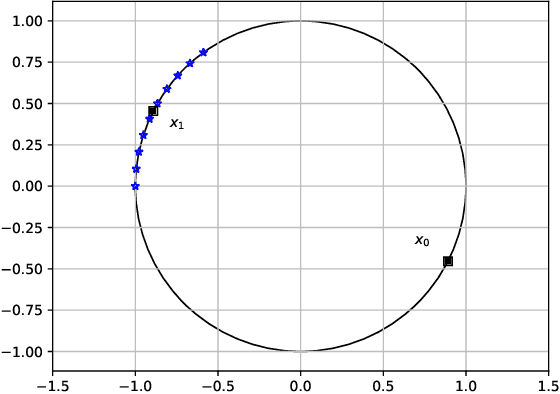
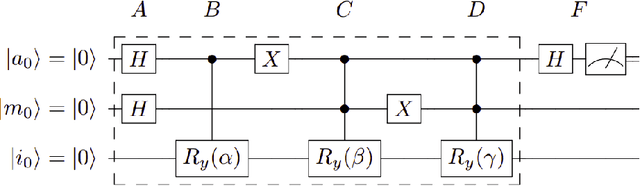
Distance-based Quantum Classifier (DBQC) is a quantum machine learning model for pattern recognition. However, DBQC has a low accuracy on real noisy quantum processors. We present a modification of DBQC named Quantum One-class Classifier (QOCC) to improve accuracy on NISQ (Noisy Intermediate-Scale Quantum) computers. Experimental results were obtained by running the proposed classifier on a computer provided by IBM Quantum Experience and show that QOCC has improved accuracy over DBQC.

Parametric Probabilistic Quantum Memory

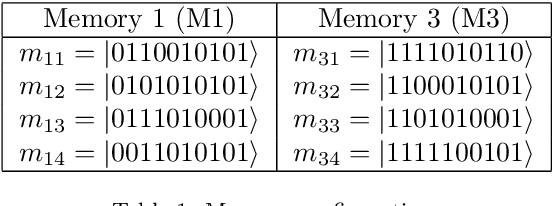
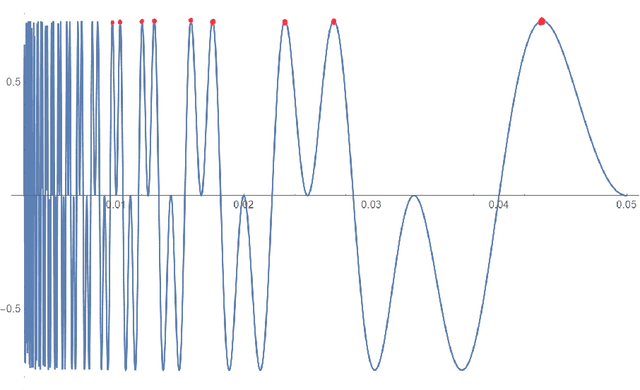
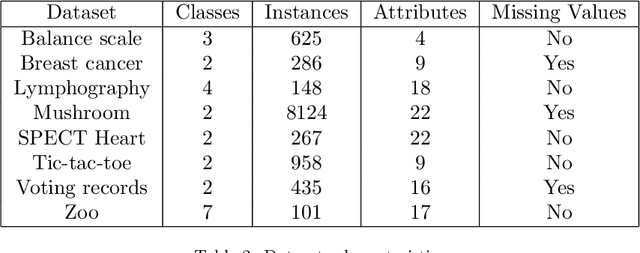
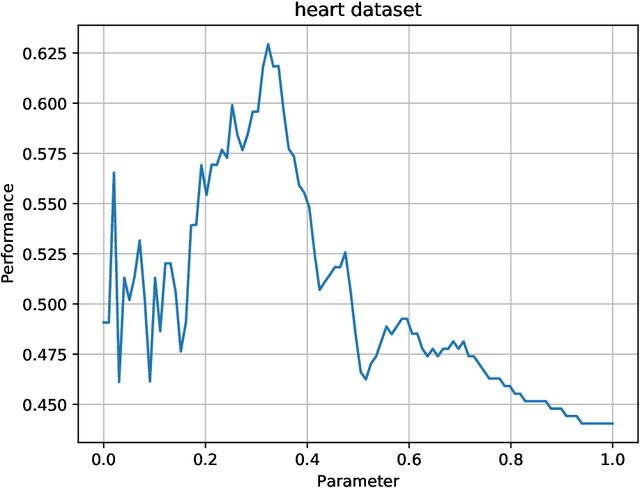
Probabilistic Quantum Memory (PQM) is a data structure that computes the distance from a binary input to all binary patterns stored in superposition on the memory. This data structure allows the development of heuristics to speed up artificial neural networks architecture selection. In this work, we propose an improved parametric version of the PQM to perform pattern classification, and we also present a PQM quantum circuit suitable for Noisy Intermediate Scale Quantum (NISQ) computers. We present a classical evaluation of a parametric PQM network classifier on public benchmark datasets. We also perform experiments to verify the viability of PQM on a 5-qubit quantum computer.

Quantum perceptron over a field and neural network architecture selection in a quantum computer

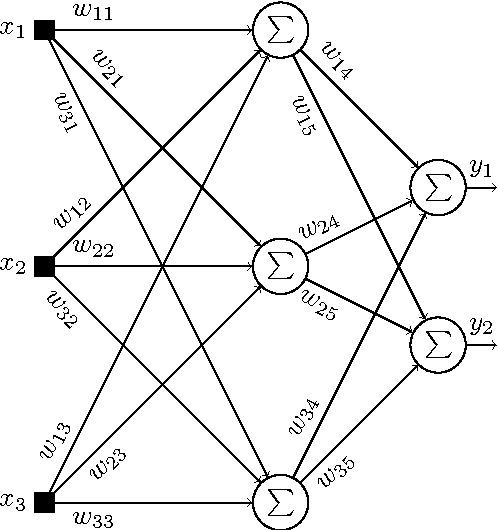
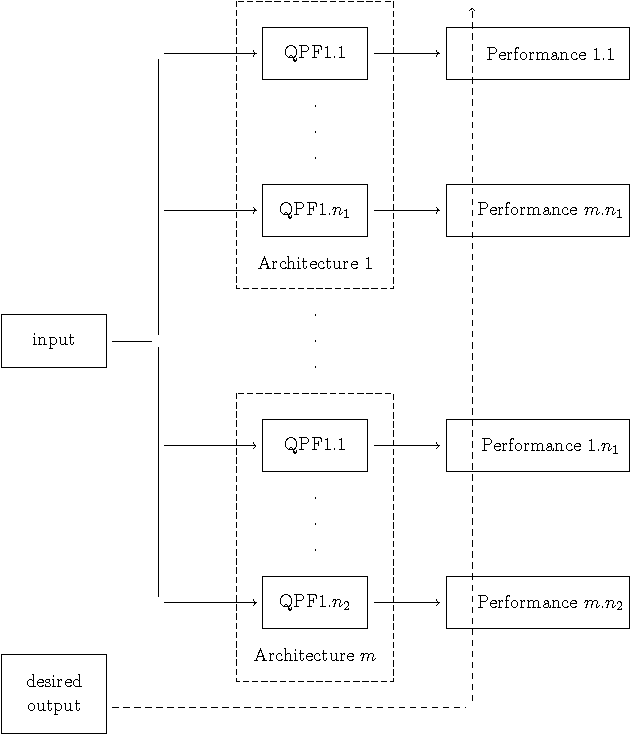
In this work, we propose a quantum neural network named quantum perceptron over a field (QPF). Quantum computers are not yet a reality and the models and algorithms proposed in this work cannot be simulated in actual (or classical) computers. QPF is a direct generalization of a classical perceptron and solves some drawbacks found in previous models of quantum perceptrons. We also present a learning algorithm named Superposition based Architecture Learning algorithm (SAL) that optimizes the neural network weights and architectures. SAL searches for the best architecture in a finite set of neural network architectures with linear time over the number of patterns in the training set. SAL is the first learning algorithm to determine neural network architectures in polynomial time. This speedup is obtained by the use of quantum parallelism and a non-linear quantum operator.

Weightless neural network parameters and architecture selection in a quantum computer

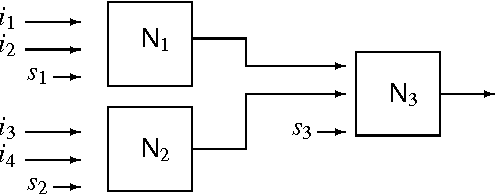
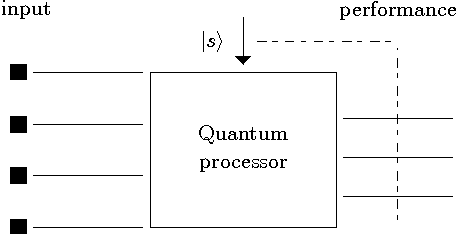
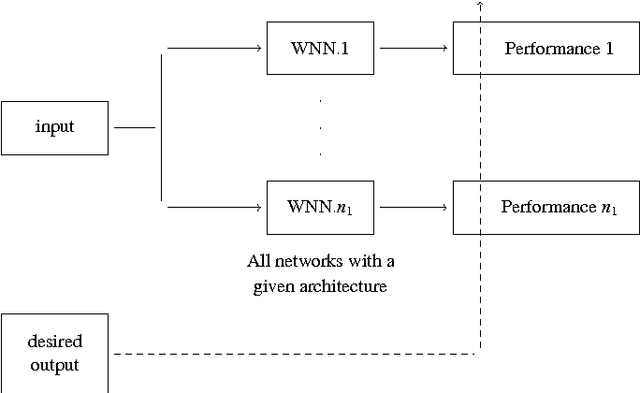
Training artificial neural networks requires a tedious empirical evaluation to determine a suitable neural network architecture. To avoid this empirical process several techniques have been proposed to automatise the architecture selection process. In this paper, we propose a method to perform parameter and architecture selection for a quantum weightless neural network (qWNN). The architecture selection is performed through the learning procedure of a qWNN with a learning algorithm that uses the principle of quantum superposition and a non-linear quantum operator. The main advantage of the proposed method is that it performs a global search in the space of qWNN architecture and parameters rather than a local search.