Wei-Guo Zhang
Consistency and Consensus Driven for Hesitant Fuzzy Linguistic Decision Making with Pairwise Comparisons
Nov 07, 2021



Abstract:Hesitant fuzzy linguistic preference relation (HFLPR) is of interest because it provides an efficient way for opinion expression under uncertainty. For enhancing the theory of decision making with HFLPR, the paper introduces an algorithm for group decision making with HFLPRs based on the acceptable consistency and consensus measurements, which involves (1) defining a hesitant fuzzy linguistic geometric consistency index (HFLGCI) and proposing a procedure for consistency checking and inconsistency improving for HFLPR; (2) measuring the group consensus based on the similarity between the original individual HFLPRs and the overall perfect HFLPR, then establishing a procedure for consensus ensuring including the determination of decision-makers weights. The convergence and monotonicity of the proposed two procedures have been proved. Some experiments are furtherly performed to investigate the critical values of the defined HFLGCI, and comparative analyses are conducted to show the effectiveness of the proposed algorithm. A case concerning the performance evaluation of venture capital guiding funds is given to illustrate the availability of the proposed algorithm. As an application of our work, an online decision-making portal is finally provided for decision-makers to utilize the proposed algorithms to solve decision-making problems.
A modified axiomatic foundation of the analytic hierarchy process
Jul 06, 2020

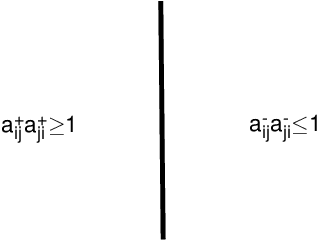

Abstract:This paper reports a modified axiomatic foundation of the analytic hierarchy process (AHP), where the reciprocal property of paired comparisons is broken. The novel concept of reciprocal symmetry breaking is proposed to characterize the considered situation without reciprocal property. It is found that the uncertainty experienced by the decision maker can be naturally incorporated into the modified axioms. Some results are derived from the new axioms involving the new concept of approximate consistency and the method of eliciting priorities. The phenomenon of ranking reversal is revisited from a theoretical viewpoint under the modified axiomatic foundation. The situations without ranking reversal are addressed and called ranking equilibrium. The likelihood of ranking reversal is captured by introducing a possibility degree index based on the Kendall's coefficient of concordance. The modified axioms and the derived facts form a novel operational basis of the AHP choice model under some uncertainty. The observations reveal that a more flexible expression of decision information could be accepted as compared to the judgments with reciprocal property.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge