A modified axiomatic foundation of the analytic hierarchy process
Paper and Code
Jul 06, 2020

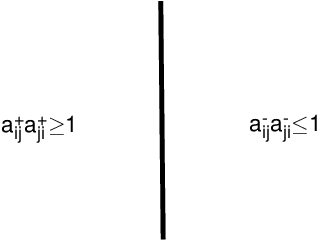

This paper reports a modified axiomatic foundation of the analytic hierarchy process (AHP), where the reciprocal property of paired comparisons is broken. The novel concept of reciprocal symmetry breaking is proposed to characterize the considered situation without reciprocal property. It is found that the uncertainty experienced by the decision maker can be naturally incorporated into the modified axioms. Some results are derived from the new axioms involving the new concept of approximate consistency and the method of eliciting priorities. The phenomenon of ranking reversal is revisited from a theoretical viewpoint under the modified axiomatic foundation. The situations without ranking reversal are addressed and called ranking equilibrium. The likelihood of ranking reversal is captured by introducing a possibility degree index based on the Kendall's coefficient of concordance. The modified axioms and the derived facts form a novel operational basis of the AHP choice model under some uncertainty. The observations reveal that a more flexible expression of decision information could be accepted as compared to the judgments with reciprocal property.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge