Estimation & Recognition under Perspective of Random-Fuzzy Dual Interpretation of Unknown Quantity: with Demonstration of IMM Filter

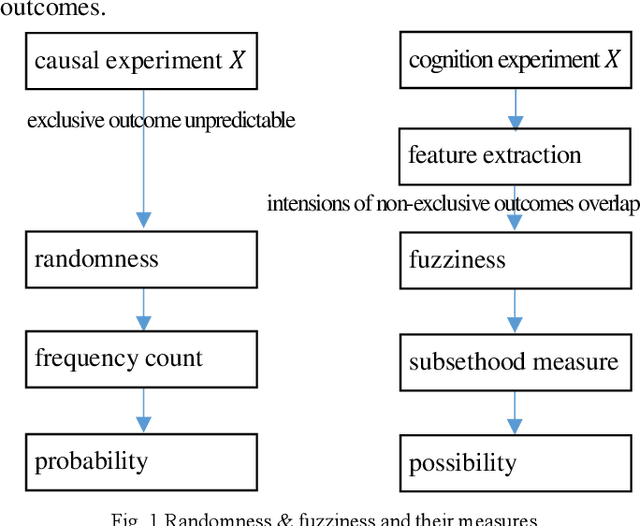
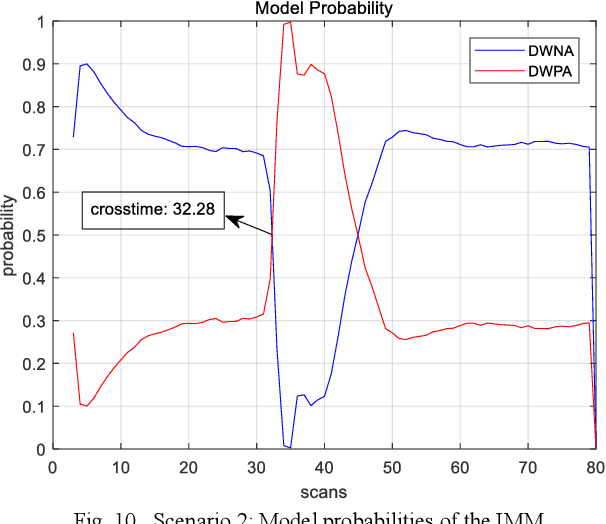
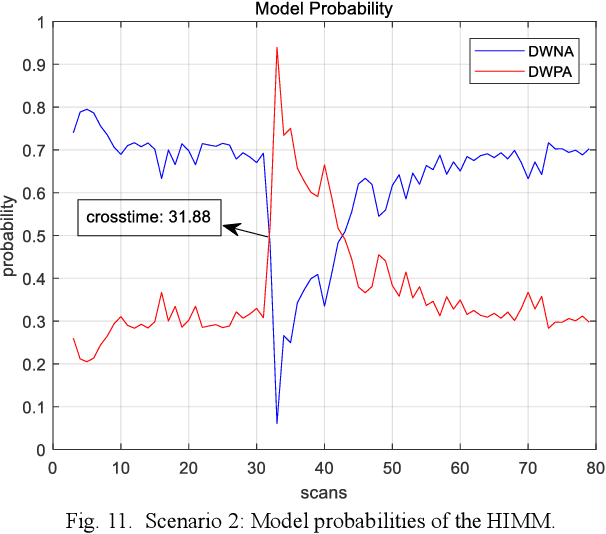
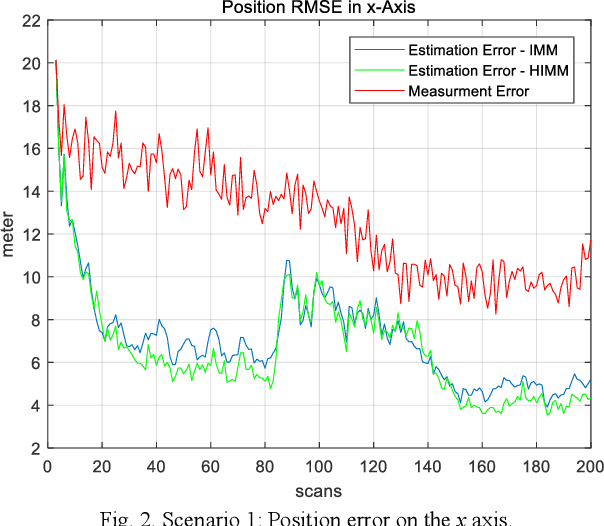
This paper is to consider the problems of estimation and recognition from the perspective of sigma-max inference (probability-possibility inference), with a focus on discovering whether some of the unknown quantities involved could be more faithfully modeled as fuzzy uncertainty. Two related key issues are addressed: 1) the random-fuzzy dual interpretation of unknown quantity being estimated; 2) the principle of selecting sigma-max operator for practical problems, such as estimation and recognition. Our perspective, conceived from definitions of randomness and fuzziness, is that continuous unknown quantity involved in estimation with inaccurate prior should be more appropriately modeled as randomness and handled by sigma inference; whereas discrete unknown quantity involved in recognition with insufficient (and inaccurate) prior could be better modeled as fuzziness and handled by max inference. The philosophy was demonstrated by an updated version of the well-known interacting multiple model (IMM) filter, for which the jump Markovian System is reformulated as a hybrid uncertainty system, with continuous state evolution modeled as usual as model-conditioned stochastic system and discrete mode transitions modeled as fuzzy system by a possibility (instead of probability) transition matrix, and hypotheses mixing is conducted by using the operation of "max" instead of "sigma". For our example of maneuvering target tracking using simulated data from both a short-range fire control radar and a long-range surveillance radar, the updated IMM filter shows significant improvement over the classic IMM filter, due to its peculiarity of hard decision of system model and a faster response to the transition of discrete mode.

The Sigma-Max System Induced from Randomness and Fuzziness

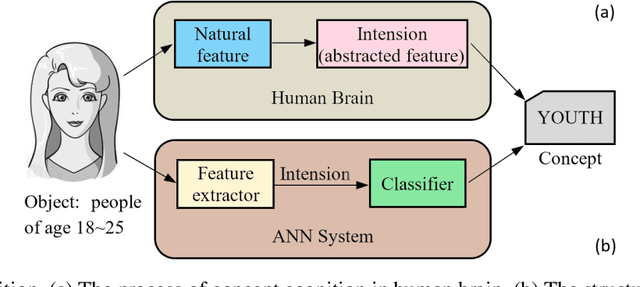
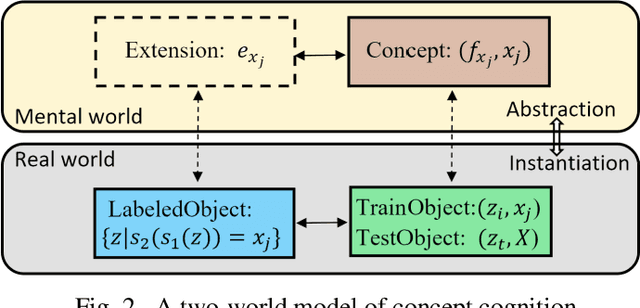
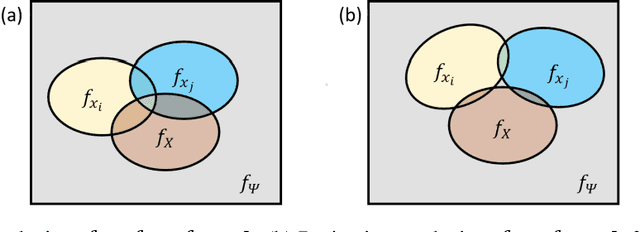
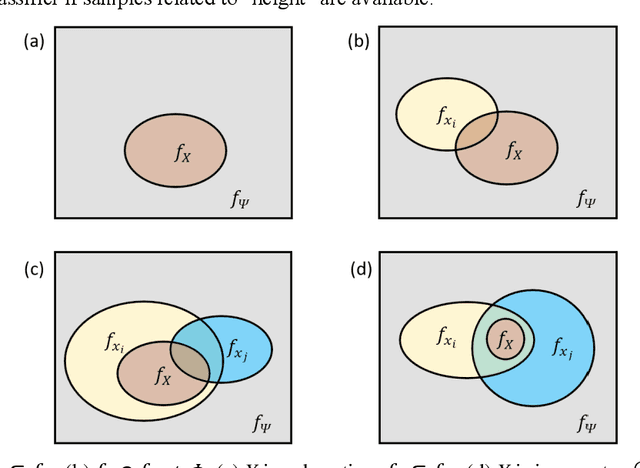
This paper managed to induce probability theory (sigma system) and possibility theory (max system) respectively from randomness and fuzziness, through which the premature theory of possibility is expected to be well founded. Such an objective is achieved by addressing three open key issues: a) the lack of clear mathematical definitions of randomness and fuzziness; b) the lack of intuitive mathematical definition of possibility; c) the lack of abstraction procedure of the axiomatic definitions of probability/possibility from their intuitive definitions. Especially, the last issue involves the question why the key axiom of "maxitivity" is adopted for possibility measure. By taking advantage of properties of the well-defined randomness and fuzziness, we derived the important conclusion that "max" is the only but un-strict disjunctive operator that is applicable across the fuzzy event space, and is an exact operator for fuzzy feature extraction that assures the max inference is an exact mechanism. It is fair to claim that the long-standing problem of lack of consensus to the foundation of possibility theory is well resolved, which would facilitate wider adoption of possibility theory in practice and promote cross prosperity of the two uncertainty theories of probability and possibility.