SA-EMO: Structure-Aligned Encoder Mixture of Operators for Generalizable Full-waveform Inversion

Full-waveform inversion (FWI) can produce high-resolution subsurface models, yet it remains inherently ill-posed, highly nonlinear, and computationally intensive. Although recent deep learning and numerical acceleration methods have improved speed and scalability, they often rely on single CNN architectures or single neural operators, which struggle to generalize in unknown or complex geological settings and are ineffective at distinguishing diverse geological types. To address these issues, we propose a Structure-Aligned Encoder-Mixture-of-Operators (SA-EMO) architecture for velocity-field inversion under unknown subsurface structures. First, a structure-aligned encoder maps high-dimensional seismic wavefields into a physically consistent latent space, thereby eliminating spatio-temporal mismatch between the waveform and velocity domains, recovering high-frequency components, and enhancing feature generalization. Then, an adaptive routing mechanism selects and fuses multiple neural-operator experts, including spectral, wavelet, multiscale, and local operators, to predict the velocity model. We systematically evaluate our approach on the OpenFWI benchmark and the Marmousi2 dataset. Results show that SA-EMO significantly outperforms traditional CNN or single-operator methods, achieving an average MAE reduction of approximately 58.443% and an improvement in boundary resolution of about 10.308%. Ablation studies further reveal that the structure-aligned encoder, the expert-fusion mechanism, and the routing module each contribute markedly to the performance gains. This work introduces a new paradigm for efficient, scalable, and physically interpretable full-waveform inversion.

Network2Vec Learning Node Representation Based on Space Mapping in Networks

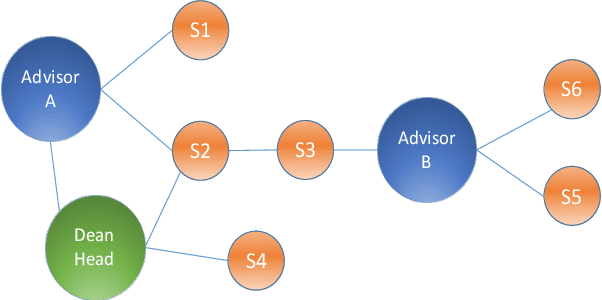
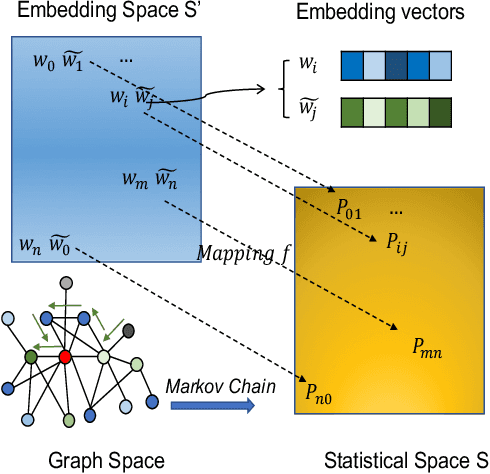
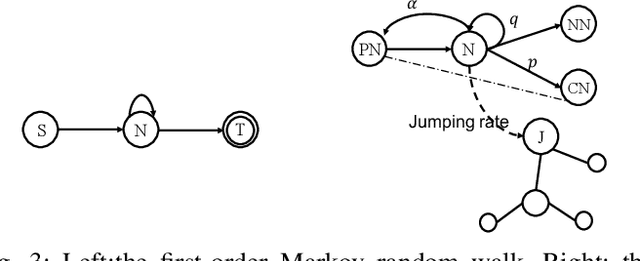
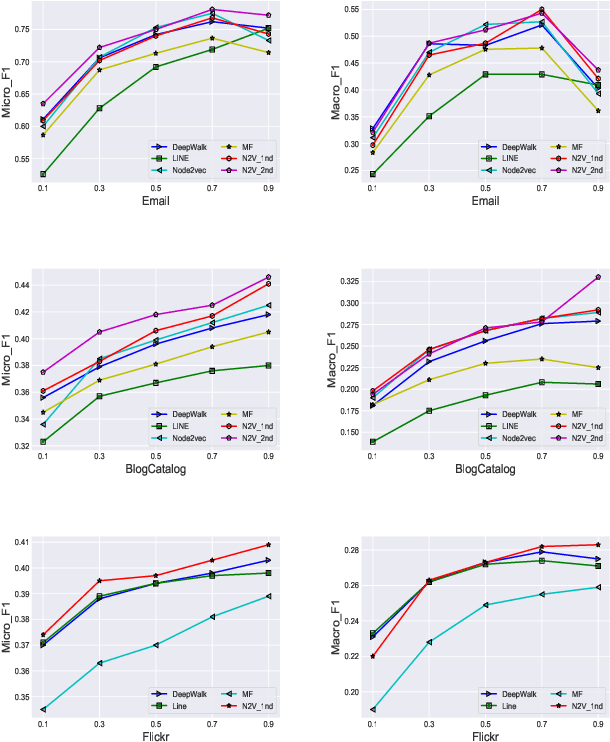
Complex networks represented as node adjacency matrices constrains the application of machine learning and parallel algorithms. To address this limitation, network embedding (i.e., graph representation) has been intensively studied to learn a fixed-length vector for each node in an embedding space, where the node properties in the original graph are preserved. Existing methods mainly focus on learning embedding vectors to preserve nodes proximity, i.e., nodes next to each other in the graph space should also be closed in the embedding space, but do not enforce algebraic statistical properties to be shared between the embedding space and graph space. In this work, we propose a lightweight model, entitled Network2Vec, to learn network embedding on the base of semantic distance mapping between the graph space and embedding space. The model builds a bridge between the two spaces leveraging the property of group homomorphism. Experiments on different learning tasks, including node classification, link prediction, and community visualization, demonstrate the effectiveness and efficiency of the new embedding method, which improves the state-of-the-art model by 19% in node classification and 7% in link prediction tasks at most. In addition, our method is significantly faster, consuming only a fraction of the time used by some famous methods.