Network2Vec Learning Node Representation Based on Space Mapping in Networks
Paper and Code
Oct 23, 2019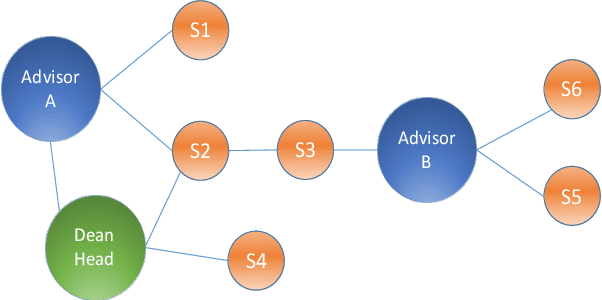
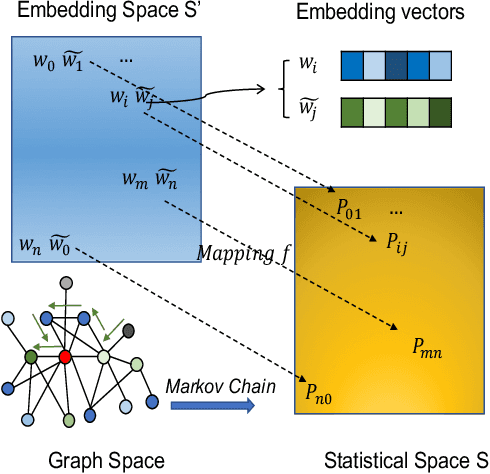
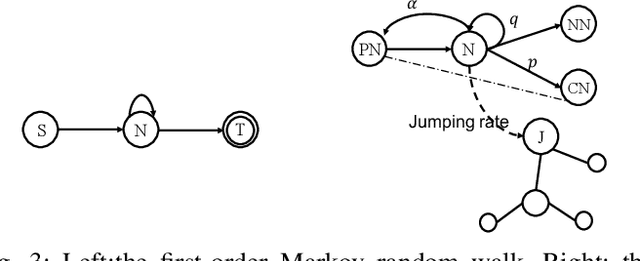
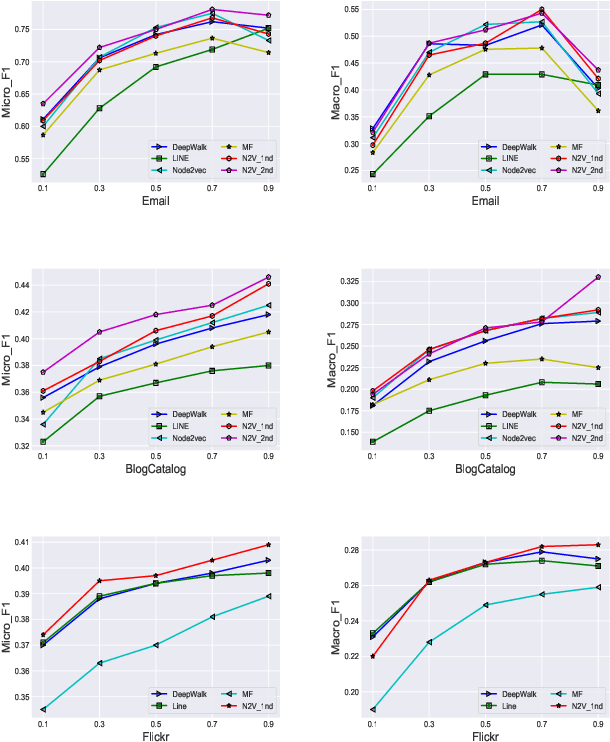
Complex networks represented as node adjacency matrices constrains the application of machine learning and parallel algorithms. To address this limitation, network embedding (i.e., graph representation) has been intensively studied to learn a fixed-length vector for each node in an embedding space, where the node properties in the original graph are preserved. Existing methods mainly focus on learning embedding vectors to preserve nodes proximity, i.e., nodes next to each other in the graph space should also be closed in the embedding space, but do not enforce algebraic statistical properties to be shared between the embedding space and graph space. In this work, we propose a lightweight model, entitled Network2Vec, to learn network embedding on the base of semantic distance mapping between the graph space and embedding space. The model builds a bridge between the two spaces leveraging the property of group homomorphism. Experiments on different learning tasks, including node classification, link prediction, and community visualization, demonstrate the effectiveness and efficiency of the new embedding method, which improves the state-of-the-art model by 19% in node classification and 7% in link prediction tasks at most. In addition, our method is significantly faster, consuming only a fraction of the time used by some famous methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge