Vincent Lefieux
Clustering high dimensional meteorological scenarios: results and performance index
Dec 14, 2020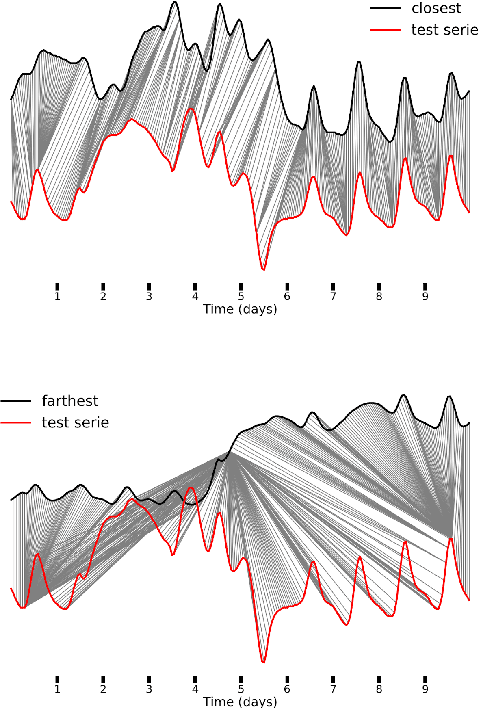
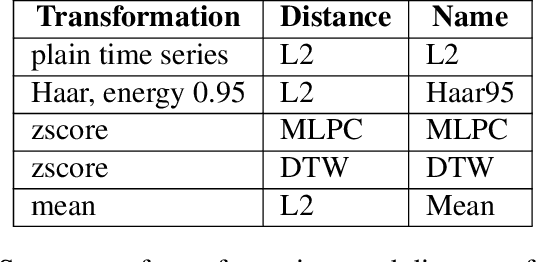
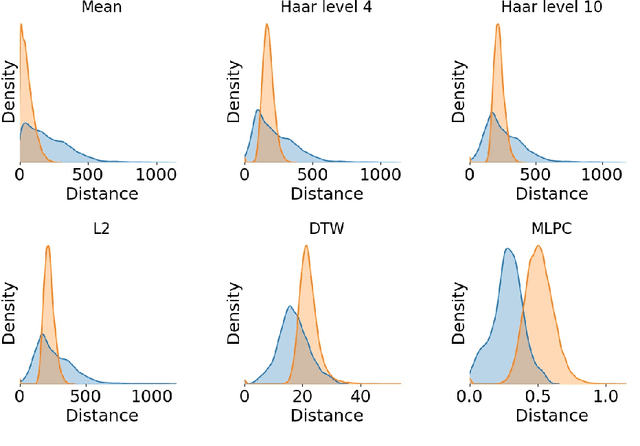
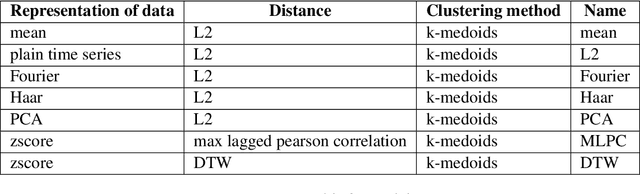
Abstract:The Reseau de Transport d'Electricit\'e (RTE) is the French main electricity network operational manager and dedicates large number of resources and efforts towards understanding climate time series data. We discuss here the problem and the methodology of grouping and selecting representatives of possible climate scenarios among a large number of climate simulations provided by RTE. The data used is composed of temperature times series for 200 different possible scenarios on a grid of geographical locations in France. These should be clustered in order to detect common patterns regarding temperatures curves and help to choose representative scenarios for network simulations, which in turn can be used for energy optimisation. We first show that the choice of the distance used for the clustering has a strong impact on the meaning of the results: depending on the type of distance used, either spatial or temporal patterns prevail. Then we discuss the difficulty of fine-tuning the distance choice (combined with a dimension reduction procedure) and we propose a methodology based on a carefully designed index.
Uncovering differential equations from data with hidden variables
Feb 06, 2020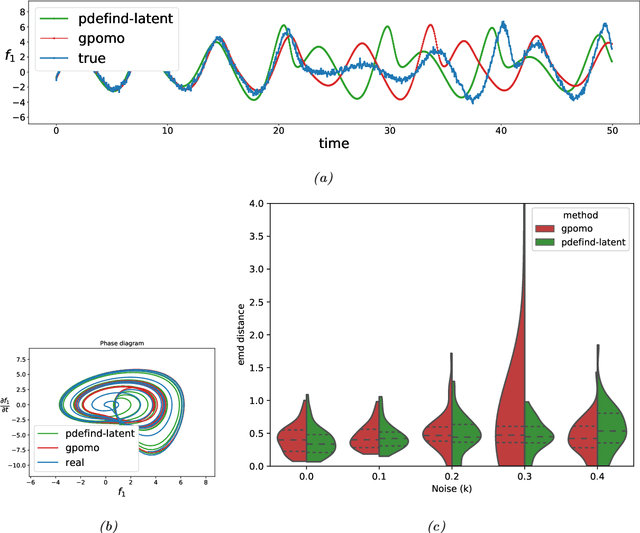
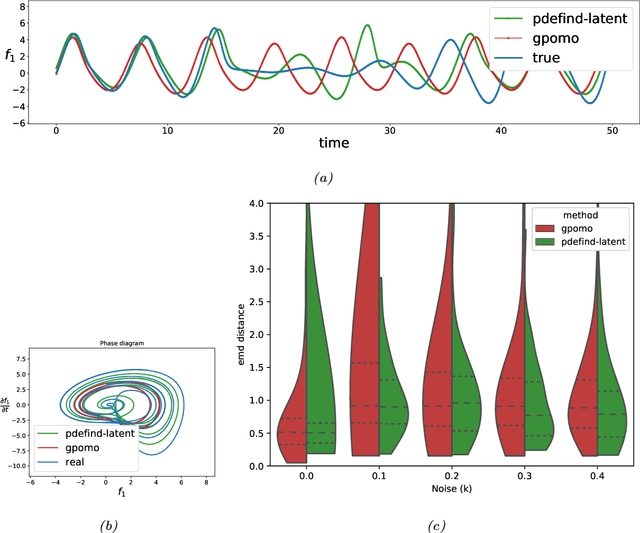
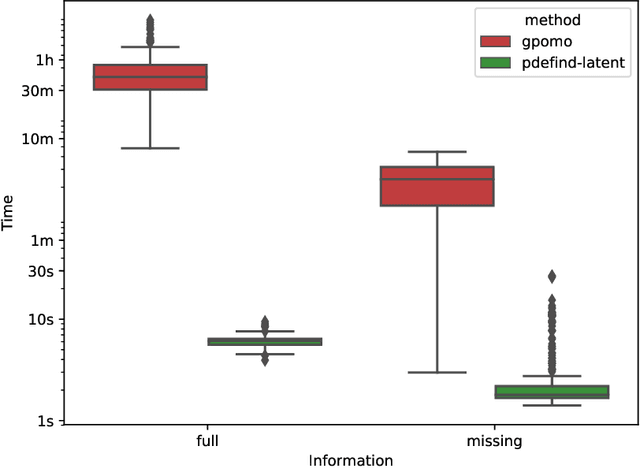
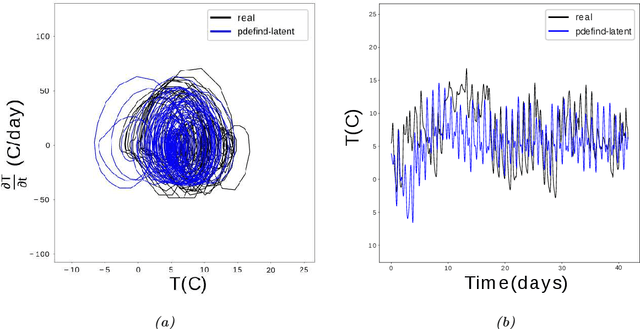
Abstract:Finding a set of differential equations to model dynamical systems is a difficult task present in many branches of science and engineering. We propose a method to learn systems of differential equations directly from data. Our method is based on solving a tailor-made $\ell_1-$regularised least-squares problem and can deal with latent variables by adding higher-order derivatives to account for the lack of information. Extensive numerical studies show that our method can recover useful representations of the dynamical system that generated the data even when some variables are not observed. Moreover, being based on solving a convex optimisation problem, our method is much faster than competing approaches based on solving combinatorial problems. Finally, we apply our methodology to a real data-set of temperature time series.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge