Agustín Somacal
State estimation of urban air pollution with statistical, physical, and super-learning graph models
Feb 05, 2024



Abstract:We consider the problem of real-time reconstruction of urban air pollution maps. The task is challenging due to the heterogeneous sources of available data, the scarcity of direct measurements, the presence of noise, and the large surfaces that need to be considered. In this work, we introduce different reconstruction methods based on posing the problem on city graphs. Our strategies can be classified as fully data-driven, physics-driven, or hybrid, and we combine them with super-learning models. The performance of the methods is tested in the case of the inner city of Paris, France.
Uncovering differential equations from data with hidden variables
Feb 06, 2020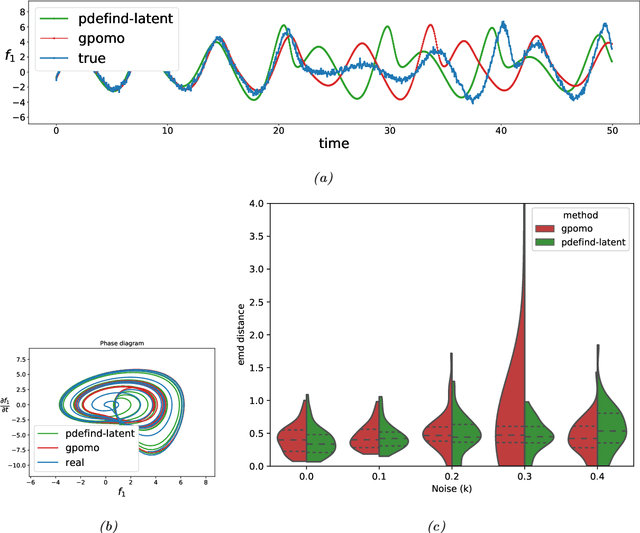
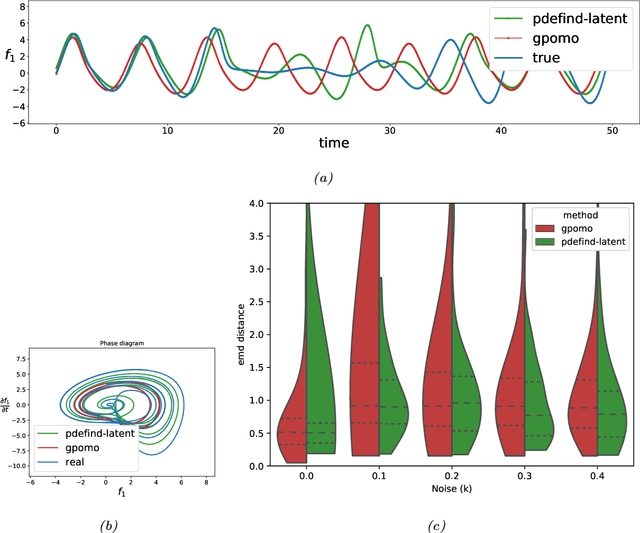
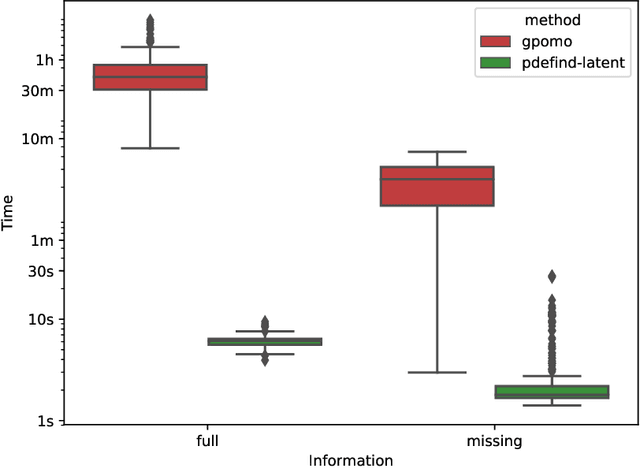
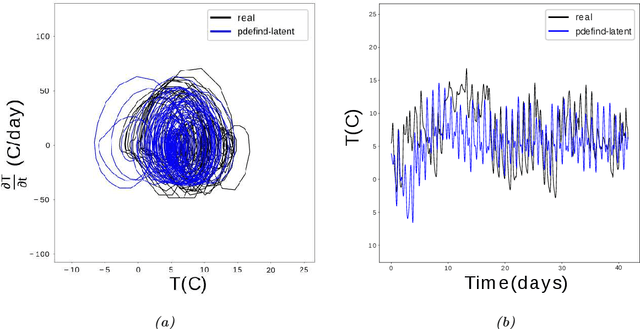
Abstract:Finding a set of differential equations to model dynamical systems is a difficult task present in many branches of science and engineering. We propose a method to learn systems of differential equations directly from data. Our method is based on solving a tailor-made $\ell_1-$regularised least-squares problem and can deal with latent variables by adding higher-order derivatives to account for the lack of information. Extensive numerical studies show that our method can recover useful representations of the dynamical system that generated the data even when some variables are not observed. Moreover, being based on solving a convex optimisation problem, our method is much faster than competing approaches based on solving combinatorial problems. Finally, we apply our methodology to a real data-set of temperature time series.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge