sigmoidF1: A Smooth F1 Score Surrogate Loss for Multilabel Classification

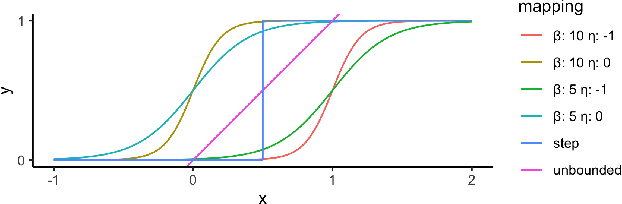
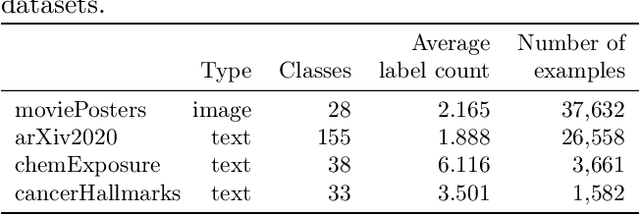
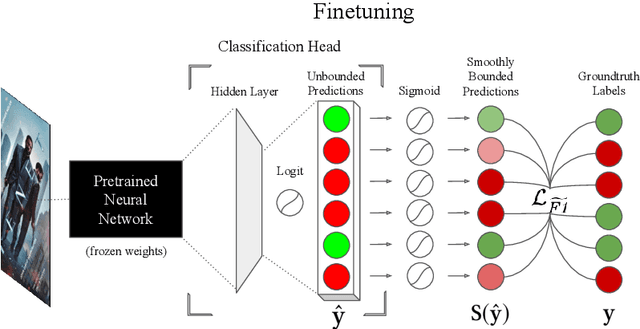
Multiclass multilabel classification refers to the task of attributing multiple labels to examples via predictions. Current models formulate a reduction of that multilabel setting into either multiple binary classifications or multiclass classification, allowing for the use of existing loss functions (sigmoid, cross-entropy, logistic, etc.). Empirically, these methods have been reported to achieve good performance on different metrics (F1 score, Recall, Precision, etc.). Theoretically though, the multilabel classification reductions does not accommodate for the prediction of varying numbers of labels per example and the underlying losses are distant estimates of the performance metrics. We propose a loss function, sigmoidF1. It is an approximation of the F1 score that (I) is smooth and tractable for stochastic gradient descent, (II) naturally approximates a multilabel metric, (III) estimates label propensities and label counts. More generally, we show that any confusion matrix metric can be formulated with a smooth surrogate. We evaluate the proposed loss function on different text and image datasets, and with a variety of metrics, to account for the complexity of multilabel classification evaluation. In our experiments, we embed the sigmoidF1 loss in a classification head that is attached to state-of-the-art efficient pretrained neural networks MobileNetV2 and DistilBERT. Our experiments show that sigmoidF1 outperforms other loss functions on four datasets and several metrics. These results show the effectiveness of using inference-time metrics as loss function at training time in general and their potential on non-trivial classification problems like multilabel classification.