Desensitization and Deception in Differential Games with Asymmetric Information

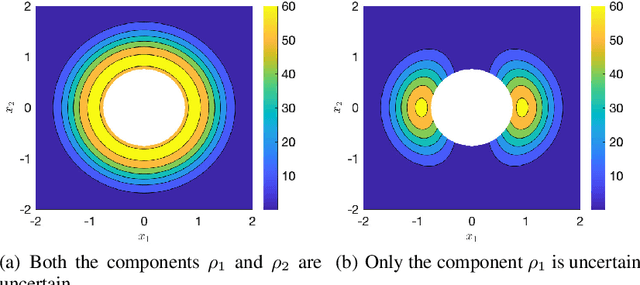
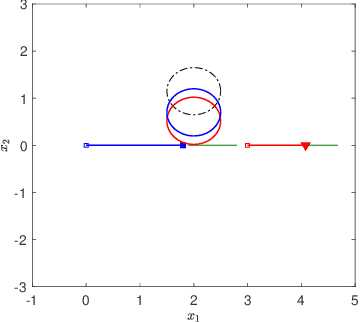
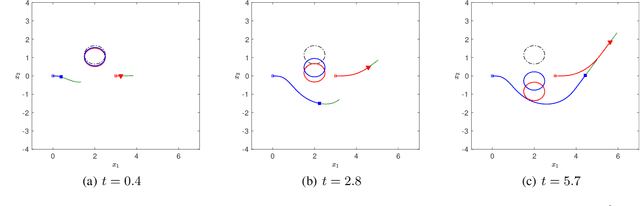
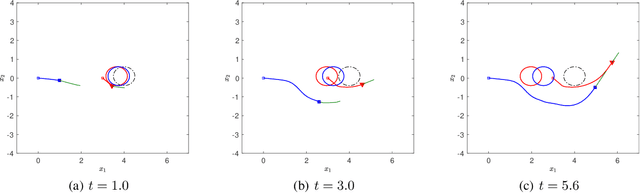
Desensitization addresses safe optimal planning under parametric uncertainties by providing sensitivity function-based risk measures. This paper expands upon the existing work on desensitization to address safe planning for a class of two-player differential games. In the proposed game, parametric uncertainties correspond to variations in a vector of model parameters about its nominal value. The two players in the proposed formulation are assumed to have information about the nominal value of the parameter vector. However, only one of the players is assumed to have complete knowledge of parametric variation, creating a form of information asymmetry in the proposed game. The lack of knowledge regarding the parametric variations is expected to result in state constraint violations for the player with an information disadvantage. In this regard, a desensitized feedback strategy that provides safe trajectories is proposed for the player with incomplete information. The proposed feedback strategy is evaluated in instances involving one pursuer and one evader with an uncertain dynamic obstacle, where the pursuer is assumed to know only the nominal value of the obstacle's speed. At the same time, the evader knows the obstacle's true speed, and also the fact that the pursuer possesses only the nominal value. Subsequently, deceptive strategies are proposed for the evader, who has an information advantage, and these strategies are assessed against the pursuer's desensitized strategy.

Apollonius Allocation Algorithm for Heterogeneous Pursuers to Capture Multiple Evaders

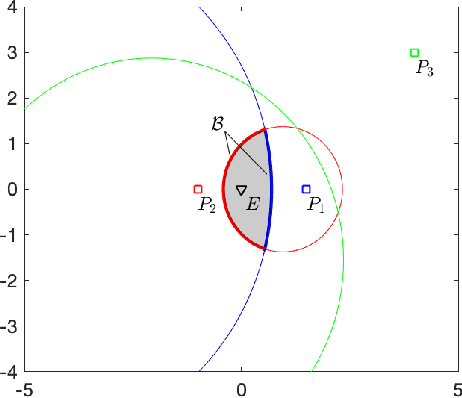
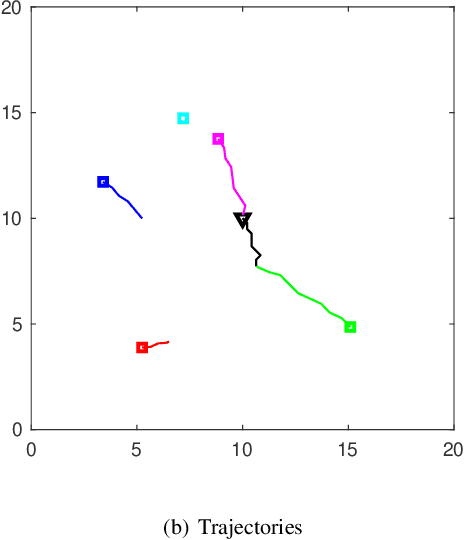
In this paper, we address pursuit-evasion problems involving multiple pursuers and multiple evaders. The pursuer and the evader teams are assumed to be heterogeneous, in the sense that each team has agents with different speed capabilities. The pursuers are all assumed to be following a constant bearing strategy. A dynamic divide and conquer approach, where at every time instant each evader is assigned to a set of pursuers based on the instantaneous positions of all the players, is introduced to solve the multi-agent pursuit problem. In this regard, the corresponding multi-pursuer single-evader problem is analyzed first. Assuming that the evader can follow any strategy, a dynamic task allocation algorithm is proposed for the pursuers. The algorithm is based on the well-known Apollonius circle and allows the pursuers to allocate their resources in an intelligent manner while guaranteeing the capture of the evader in minimum time. The proposed algorithm is then extended to assign pursuers in multi-evader settings that is proven to capture all the evaders in finite time.

Safe Optimal Control under Parametric Uncertainties

We address the issue of safe optimal path planning under parametric uncertainties using a novel regularizer that allows trading off optimality with safety. The proposed regularizer leverages the notion that collisions may be modelled as constraint violations in an optimal control setting to produce open-loop trajectories with reduced risk of collisions. The risk of constraint violation is evaluated using a state-dependent relevance function and first-order variations in the constraint function with respect to parametric variations. The approach is generic and can be adapted to any optimal control formulation that deals with constraints under parametric uncertainty. Simulations using a holonomic robot with simple dynamics avoiding multiple dynamic obstacles with uncertain velocities are used to demonstrate the effectiveness of the proposed approach. Finally, we introduce the car vs. train problem to emphasize the dependence of the resultant risk aversion behavior on the form of the constraint function used to derive the regularizer.