Desensitization and Deception in Differential Games with Asymmetric Information

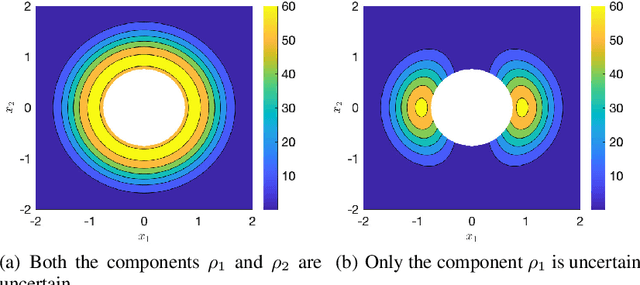
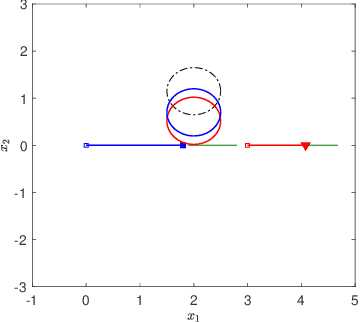
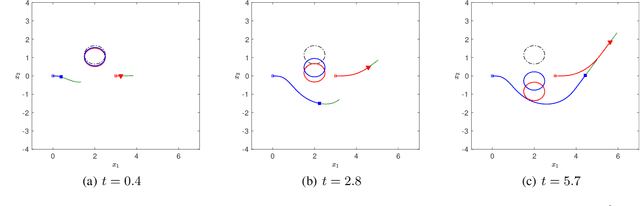
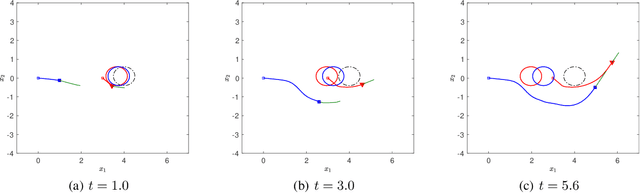
Desensitization addresses safe optimal planning under parametric uncertainties by providing sensitivity function-based risk measures. This paper expands upon the existing work on desensitization to address safe planning for a class of two-player differential games. In the proposed game, parametric uncertainties correspond to variations in a vector of model parameters about its nominal value. The two players in the proposed formulation are assumed to have information about the nominal value of the parameter vector. However, only one of the players is assumed to have complete knowledge of parametric variation, creating a form of information asymmetry in the proposed game. The lack of knowledge regarding the parametric variations is expected to result in state constraint violations for the player with an information disadvantage. In this regard, a desensitized feedback strategy that provides safe trajectories is proposed for the player with incomplete information. The proposed feedback strategy is evaluated in instances involving one pursuer and one evader with an uncertain dynamic obstacle, where the pursuer is assumed to know only the nominal value of the obstacle's speed. At the same time, the evader knows the obstacle's true speed, and also the fact that the pursuer possesses only the nominal value. Subsequently, deceptive strategies are proposed for the evader, who has an information advantage, and these strategies are assessed against the pursuer's desensitized strategy.