Apollonius Allocation Algorithm for Heterogeneous Pursuers to Capture Multiple Evaders
Paper and Code
Jun 19, 2020

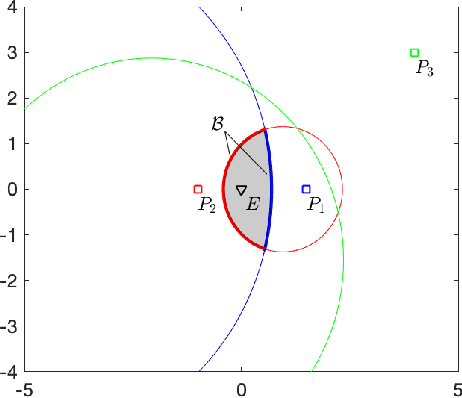
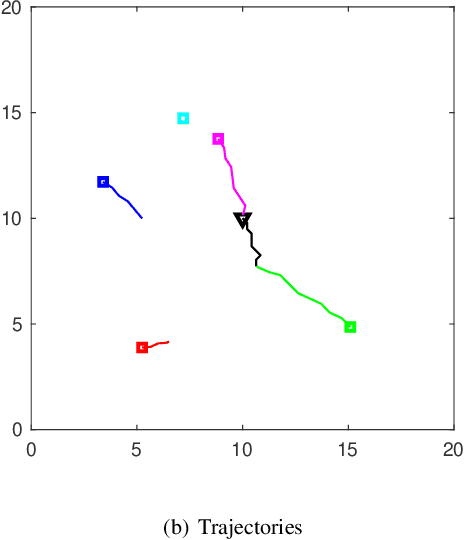
In this paper, we address pursuit-evasion problems involving multiple pursuers and multiple evaders. The pursuer and the evader teams are assumed to be heterogeneous, in the sense that each team has agents with different speed capabilities. The pursuers are all assumed to be following a constant bearing strategy. A dynamic divide and conquer approach, where at every time instant each evader is assigned to a set of pursuers based on the instantaneous positions of all the players, is introduced to solve the multi-agent pursuit problem. In this regard, the corresponding multi-pursuer single-evader problem is analyzed first. Assuming that the evader can follow any strategy, a dynamic task allocation algorithm is proposed for the pursuers. The algorithm is based on the well-known Apollonius circle and allows the pursuers to allocate their resources in an intelligent manner while guaranteeing the capture of the evader in minimum time. The proposed algorithm is then extended to assign pursuers in multi-evader settings that is proven to capture all the evaders in finite time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge