From Common Sense Reasoning to Neural Network Models through Multiple Preferences: an overview

In this paper we discuss the relationships between conditional and preferential logics and neural network models, based on a multi-preferential semantics. We propose a concept-wise multipreference semantics, recently introduced for defeasible description logics to take into account preferences with respect to different concepts, as a tool for providing a semantic interpretation to neural network models. This approach has been explored both for unsupervised neural network models (Self-Organising Maps) and for supervised ones (Multilayer Perceptrons), and we expect that the same approach might be extended to other neural network models. It allows for logical properties of the network to be checked (by model checking) over an interpretation capturing the input-output behavior of the network. For Multilayer Perceptrons, the deep network itself can be regarded as a conditional knowledge base, in which synaptic connections correspond to weighted conditionals. The paper describes the general approach, through the cases of Self-Organising Maps and Multilayer Perceptrons, and discusses some open issues and perspectives.

A conditional, a fuzzy and a probabilistic interpretation of self-organising maps

In this paper we establish a link between preferential semantics for description logics and self-organising maps, which have been proposed as possible candidates to explain the psychological mechanisms underlying category generalisation. In particular, we show that a concept-wise multipreference semantics, which takes into account preferences with respect to different concepts and has been recently proposed for defeasible description logics, can be used to to provide a logical interpretation of SOMs. We also provide a logical interpretation of SOMs in terms of a fuzzy description logic as well as a probabilistic account.

On a plausible concept-wise multipreference semantics and its relations with self-organising maps

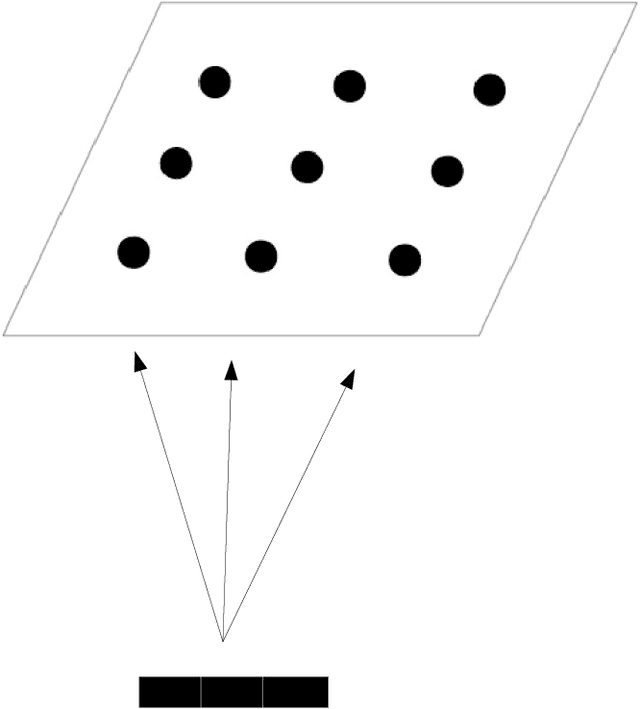
Inthispaperwedescribeaconcept-wisemulti-preferencesemantics for description logic which has its root in the preferential approach for modeling defeasible reasoning in knowledge representation. We argue that this proposal, beside satisfying some desired properties, such as KLM postulates, and avoiding the drowning problem, also defines a plausible notion of semantics. We motivate the plausibility of the concept-wise multi-preference semantics by developing a logical semantics of self-organising maps, which have been proposed as possible candidates to explain the psychological mechanisms underlying category generalisation, in terms of multi-preference interpretations.

Reasoning about Typicality and Probabilities in Preferential Description Logics

In this work we describe preferential Description Logics of typicality, a nonmonotonic extension of standard Description Logics by means of a typicality operator T allowing to extend a knowledge base with inclusions of the form T(C) v D, whose intuitive meaning is that normally/typically Cs are also Ds. This extension is based on a minimal model semantics corresponding to a notion of rational closure, built upon preferential models. We recall the basic concepts underlying preferential Description Logics. We also present two extensions of the preferential semantics: on the one hand, we consider probabilistic extensions, based on a distributed semantics that is suitable for tackling the problem of commonsense concept combination, on the other hand, we consider other strengthening of the rational closure semantics and construction to avoid the so-called blocking of property inheritance problem.

A reconstruction of the multipreference closure

The paper describes a preferential approach for dealing with exceptions in KLM preferential logics, based on the rational closure. It is well known that the rational closure does not allow an independent handling of the inheritance of different defeasible properties of concepts. Several solutions have been proposed to face this problem and the lexicographic closure is the most notable one. In this work, we consider an alternative closure construction, called the Multi Preference closure (MP-closure), that has been first considered for reasoning with exceptions in DLs. Here, we reconstruct the notion of MP-closure in the propositional case and we show that it is a natural variant of Lehmann's lexicographic closure. Abandoning Maximal Entropy (an alternative route already considered but not explored by Lehmann) leads to a construction which exploits a different lexicographic ordering w.r.t. the lexicographic closure, and determines a preferential consequence relation rather than a rational consequence relation. We show that, building on the MP-closure semantics, rationality can be recovered, at least from the semantic point of view, resulting in a rational consequence relation which is stronger than the rational closure, but incomparable with the lexicographic closure. We also show that the MP-closure is stronger than the Relevant Closure.

Reasoning about exceptions in ontologies: from the lexicographic closure to the skeptical closure

Reasoning about exceptions in ontologies is nowadays one of the challenges the description logics community is facing. The paper describes a preferential approach for dealing with exceptions in Description Logics, based on the rational closure. The rational closure has the merit of providing a simple and efficient approach for reasoning with exceptions, but it does not allow independent handling of the inheritance of different defeasible properties of concepts. In this work we outline a possible solution to this problem by introducing a variant of the lexicographical closure, that we call skeptical closure, which requires to construct a single base. We develop a bi-preference semantics semantics for defining a characterization of the skeptical closure.

Self-organizing maps and generalization: an algorithmic description of Numerosity and Variability Effects

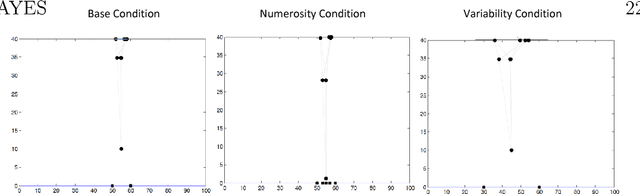
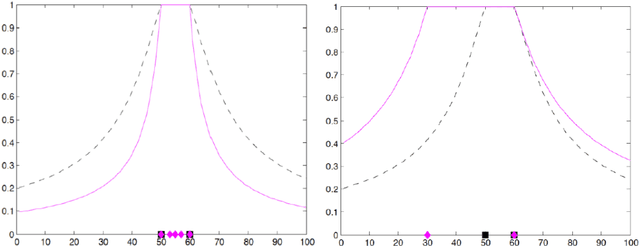
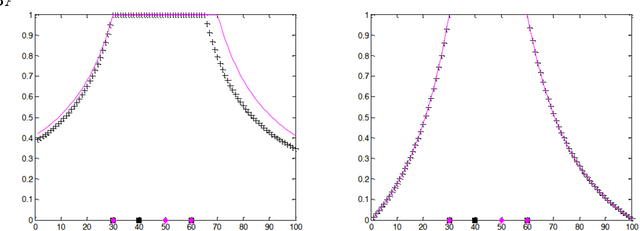
Category, or property generalization is a central function in the human cognition. It plays a crucial role in a variety of domains, such as learning, everyday reasoning, specialized reasoning, and decision making. Judging the content of a dish as edible, a hormone level as healthy, a building as belonging to the same architectural style as previously seen buildings, are examples of category generalization. In this paper, we propose self-organizing maps as candidates to explain the psychological mechanisms underlying category generalization. Self-organizing maps are psychologically and biologically plausible neural network models that learn after limited exposure to positive category examples, without any need of contrastive information. Just like humans. They reproduce human behavior in category generalization, in particular for what concerns the well-known Numerosity and Variability effects, which are usually explained with Bayesian tools. Where category generalization is concerned, self-organizing maps are good candidates to bridge the gap between the computational level of analysis in Marr's hierarchy (where Bayesian models are situated) and the algorithmic level of aanalysis in Marr's hierarchy (where Bayesian models are situated) and the algorithmic level of analysis in which plausible mechanisms are described.

Reasoning about multiple aspects in DLs: Semantics and Closure Construction

Starting from the observation that rational closure has the undesirable property of being an "all or nothing" mechanism, we here propose a multipreferential semantics, which enriches the preferential semantics underlying rational closure in order to separately deal with the inheritance of different properties in an ontology with exceptions. We provide a multipreference closure mechanism which is sound with respect to the multipreference semantics.

A strengthening of rational closure in DLs: reasoning about multiple aspects

We propose a logical analysis of the concept of typicality, central in human cognition (Rosch,1978). We start from a previously proposed extension of the basic Description Logic ALC (a computationally tractable fragment of First Order Logic, used to represent concept inclusions and ontologies) with a typicality operator T that allows to consistently represent the attribution to classes of individuals of properties with exceptions (as in the classic example (i) typical birds fly, (ii) penguins are birds but (iii) typical penguins don't fly). We then strengthen this extension in order to separately reason about the typicality with respect to different aspects (e.g., flying, having nice feather: in the previous example, penguins may not inherit the property of flying, for which they are exceptional, but can nonetheless inherit other properties, such as having nice feather).

Rational Closure in SHIQ

We define a notion of rational closure for the logic SHIQ, which does not enjoys the finite model property, building on the notion of rational closure introduced by Lehmann and Magidor in [23]. We provide a semantic characterization of rational closure in SHIQ in terms of a preferential semantics, based on a finite rank characterization of minimal models. We show that the rational closure of a TBox can be computed in EXPTIME using entailment in SHIQ.