Lecture Notes on Fair Division

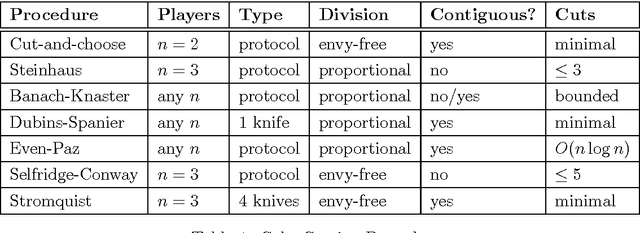
Fair division is the problem of dividing one or several goods amongst two or more agents in a way that satisfies a suitable fairness criterion. These Notes provide a succinct introduction to the field. We cover three main topics. First, we need to define what is to be understood by a "fair" allocation of goods to individuals. We present an overview of the most important fairness criteria (as well as the closely related criteria for economic efficiency) developed in the literature, together with a short discussion of their axiomatic foundations. Second, we give an introduction to cake-cutting procedures as an example of methods for fairly dividing a single divisible resource amongst a group of individuals. Third, we discuss the combinatorial optimisation problem of fairly allocating a set of indivisible goods to a group of agents, covering both centralised algorithms (similar to auctions) and a distributed approach based on negotiation. While the classical literature on fair division has largely developed within Economics, these Notes are specifically written for readers with a background in Computer Science or similar, and who may be (or may wish to be) engaged in research in Artificial Intelligence, Multiagent Systems, or Computational Social Choice. References for further reading, as well as a small number of exercises, are included. Notes prepared for a tutorial at the 11th European Agent Systems Summer School (EASSS-2009), Torino, Italy, 31 August and 1 September 2009. Updated for a tutorial at the COST-ADT Doctoral School on Computational Social Choice, Estoril, Portugal, 9--14 April 2010.

Preservation of Semantic Properties during the Aggregation of Abstract Argumentation Frameworks

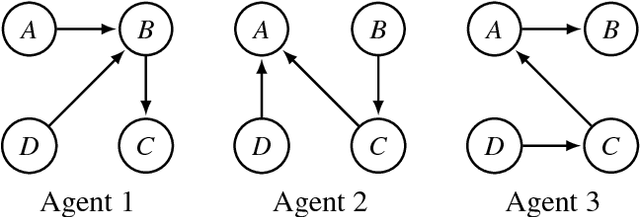
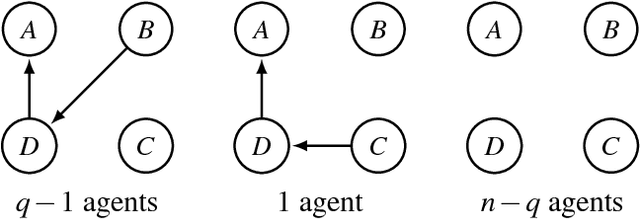
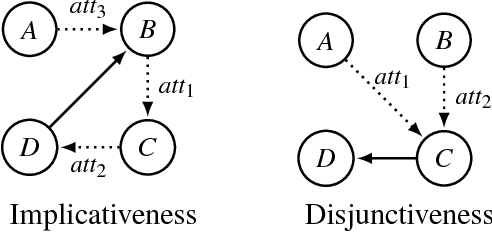
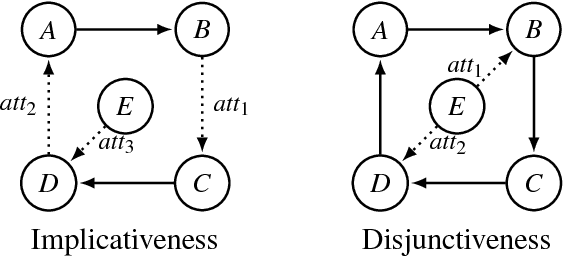
An abstract argumentation framework can be used to model the argumentative stance of an agent at a high level of abstraction, by indicating for every pair of arguments that is being considered in a debate whether the first attacks the second. When modelling a group of agents engaged in a debate, we may wish to aggregate their individual argumentation frameworks to obtain a single such framework that reflects the consensus of the group. Even when agents disagree on many details, there may well be high-level agreement on important semantic properties, such as the acceptability of a given argument. Using techniques from social choice theory, we analyse under what circumstances such semantic properties agreed upon by the individual agents can be preserved under aggregation.

Graph Aggregation

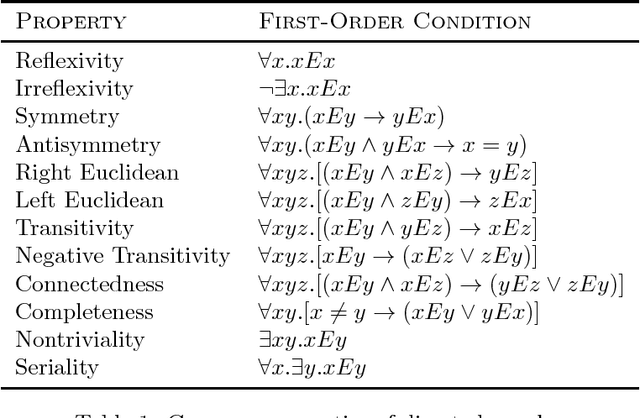
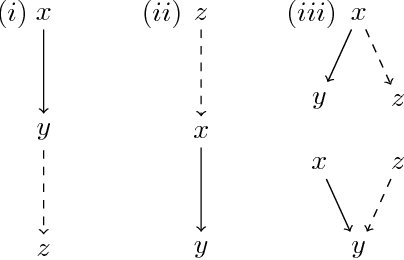
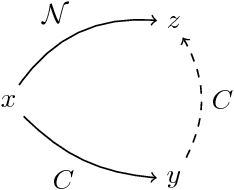
Graph aggregation is the process of computing a single output graph that constitutes a good compromise between several input graphs, each provided by a different source. One needs to perform graph aggregation in a wide variety of situations, e.g., when applying a voting rule (graphs as preference orders), when consolidating conflicting views regarding the relationships between arguments in a debate (graphs as abstract argumentation frameworks), or when computing a consensus between several alternative clusterings of a given dataset (graphs as equivalence relations). In this paper, we introduce a formal framework for graph aggregation grounded in social choice theory. Our focus is on understanding which properties shared by the individual input graphs will transfer to the output graph returned by a given aggregation rule. We consider both common properties of graphs, such as transitivity and reflexivity, and arbitrary properties expressible in certain fragments of modal logic. Our results establish several connections between the types of properties preserved under aggregation and the choice-theoretic axioms satisfied by the rules used. The most important of these results is a powerful impossibility theorem that generalises Arrow's seminal result for the aggregation of preference orders to a large collection of different types of graphs.

Automated Search for Impossibility Theorems in Social Choice Theory: Ranking Sets of Objects

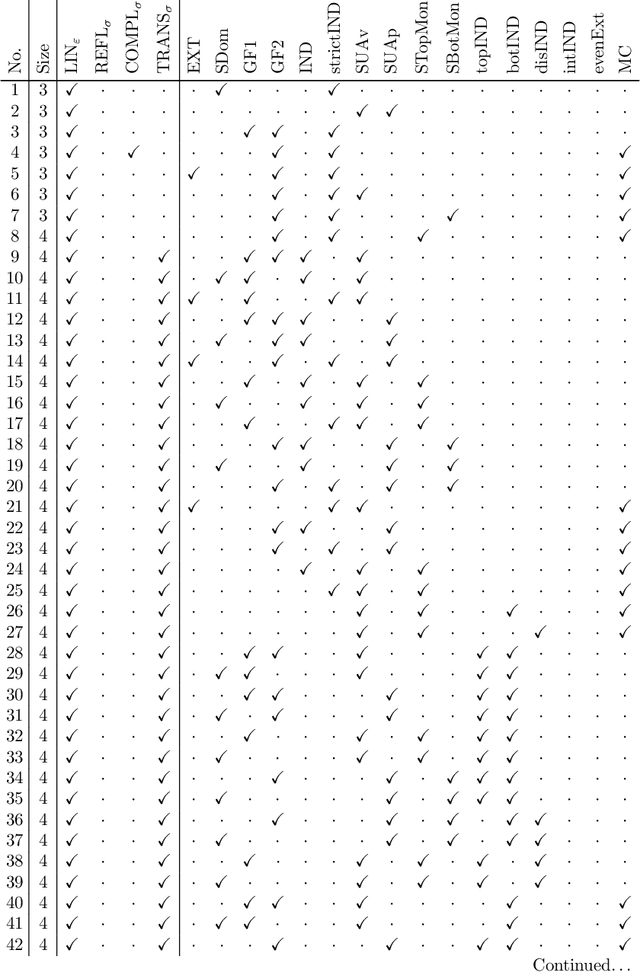
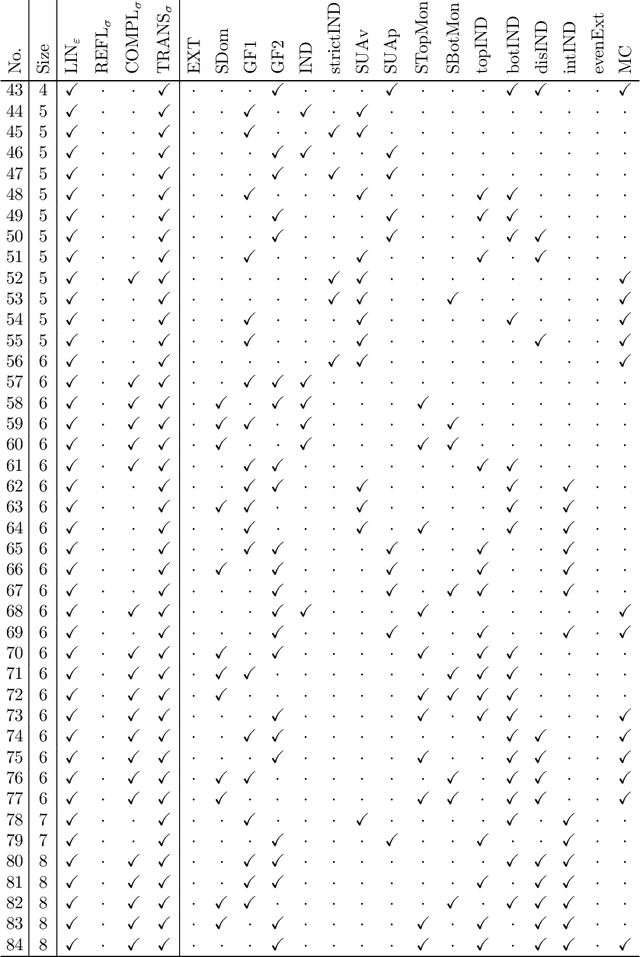
We present a method for using standard techniques from satisfiability checking to automatically verify and discover theorems in an area of economic theory known as ranking sets of objects. The key question in this area, which has important applications in social choice theory and decision making under uncertainty, is how to extend an agents preferences over a number of objects to a preference relation over nonempty sets of such objects. Certain combinations of seemingly natural principles for this kind of preference extension can result in logical inconsistencies, which has led to a number of important impossibility theorems. We first prove a general result that shows that for a wide range of such principles, characterised by their syntactic form when expressed in a many-sorted first-order logic, any impossibility exhibited at a fixed (small) domain size will necessarily extend to the general case. We then show how to formulate candidates for impossibility theorems at a fixed domain size in propositional logic, which in turn enables us to automatically search for (general) impossibility theorems using a SAT solver. When applied to a space of 20 principles for preference extension familiar from the literature, this method yields a total of 84 impossibility theorems, including both known and nontrivial new results.