Proving the Incompatibility of Efficiency and Strategyproofness via SMT Solving

Two important requirements when aggregating the preferences of multiple agents are that the outcome should be economically efficient and the aggregation mechanism should not be manipulable. In this paper, we provide a computer-aided proof of a sweeping impossibility using these two conditions for randomized aggregation mechanisms. More precisely, we show that every efficient aggregation mechanism can be manipulated for all expected utility representations of the agents' preferences. This settles an open problem and strengthens a number of existing theorems, including statements that were shown within the special domain of assignment. Our proof is obtained by formulating the claim as a satisfiability problem over predicates from real-valued arithmetic, which is then checked using an SMT (satisfiability modulo theories) solver. In order to verify the correctness of the result, a minimal unsatisfiable set of constraints returned by the SMT solver was translated back into a proof in higher-order logic, which was automatically verified by an interactive theorem prover. To the best of our knowledge, this is the first application of SMT solvers in computational social choice.

Finding Preference Profiles of Condorcet Dimension $k$ via SAT

Condorcet winning sets are a set-valued generalization of the well-known concept of a Condorcet winner. As supersets of Condorcet winning sets are always Condorcet winning sets themselves, an interesting property of preference profiles is the size of the smallest Condorcet winning set they admit. This smallest size is called the Condorcet dimension of a preference profile. Since little is known about profiles that have a certain Condorcet dimension, we show in this paper how the problem of finding a preference profile that has a given Condorcet dimension can be encoded as a satisfiability problem and solved by a SAT solver. Initial results include a minimal example of a preference profile of Condorcet dimension 3, improving previously known examples both in terms of the number of agents as well as alternatives. Due to the high complexity of such problems it remains open whether a preference profile of Condorcet dimension 4 exists.

Automated Search for Impossibility Theorems in Social Choice Theory: Ranking Sets of Objects

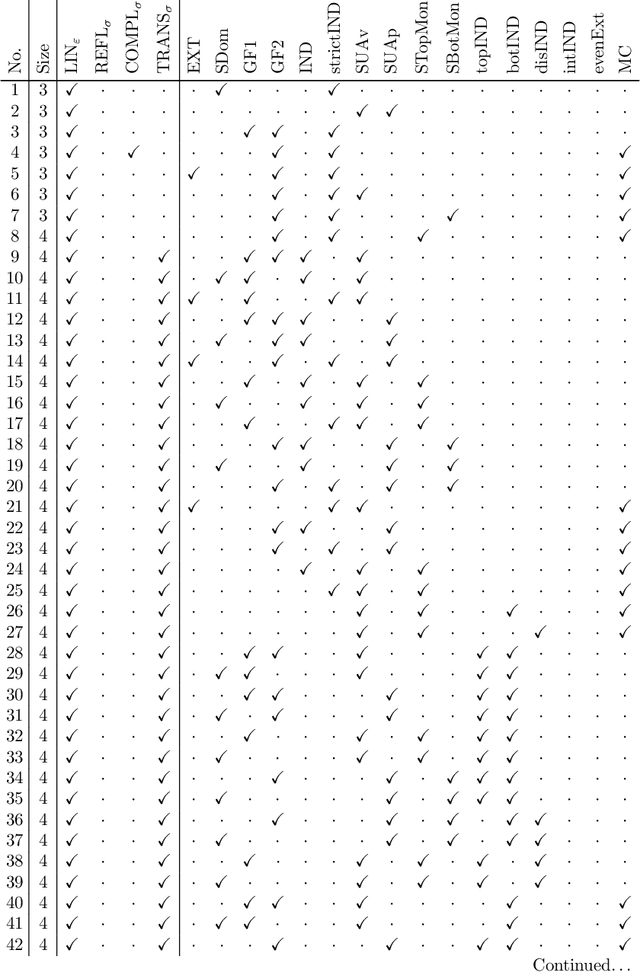
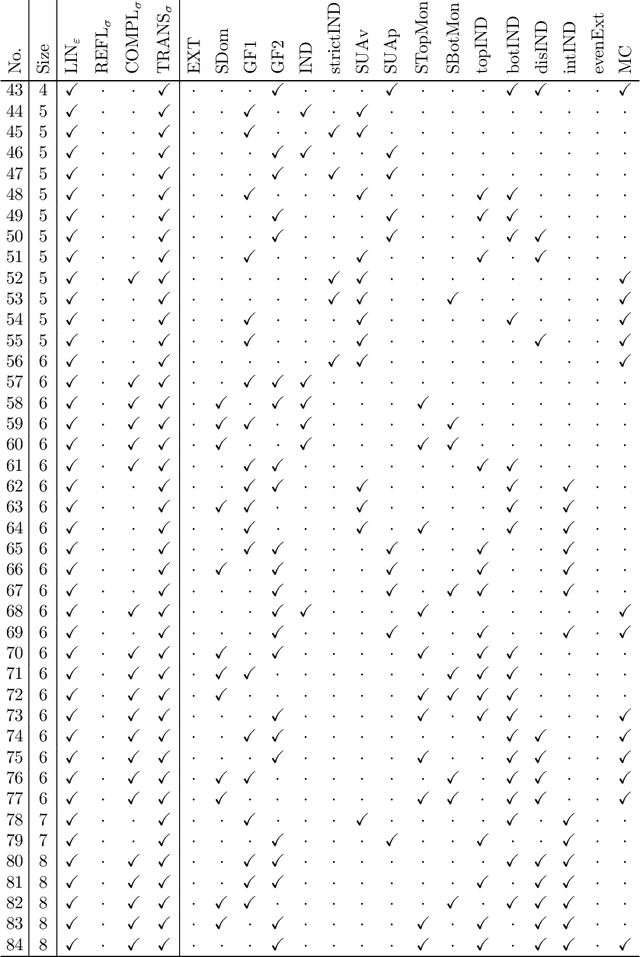
We present a method for using standard techniques from satisfiability checking to automatically verify and discover theorems in an area of economic theory known as ranking sets of objects. The key question in this area, which has important applications in social choice theory and decision making under uncertainty, is how to extend an agents preferences over a number of objects to a preference relation over nonempty sets of such objects. Certain combinations of seemingly natural principles for this kind of preference extension can result in logical inconsistencies, which has led to a number of important impossibility theorems. We first prove a general result that shows that for a wide range of such principles, characterised by their syntactic form when expressed in a many-sorted first-order logic, any impossibility exhibited at a fixed (small) domain size will necessarily extend to the general case. We then show how to formulate candidates for impossibility theorems at a fixed domain size in propositional logic, which in turn enables us to automatically search for (general) impossibility theorems using a SAT solver. When applied to a space of 20 principles for preference extension familiar from the literature, this method yields a total of 84 impossibility theorems, including both known and nontrivial new results.