Adaptive Graph-based Total Variation for Tomographic Reconstructions

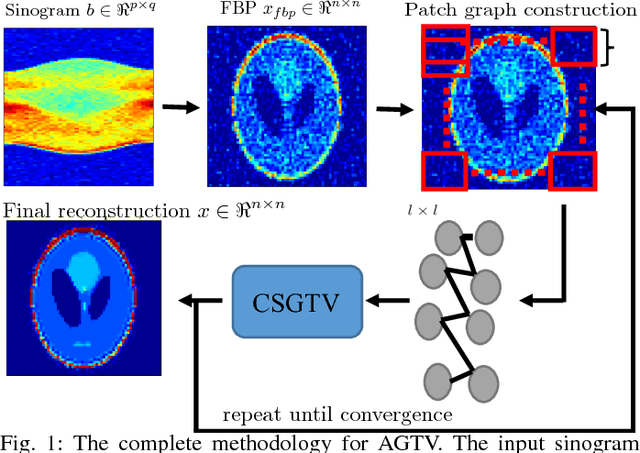
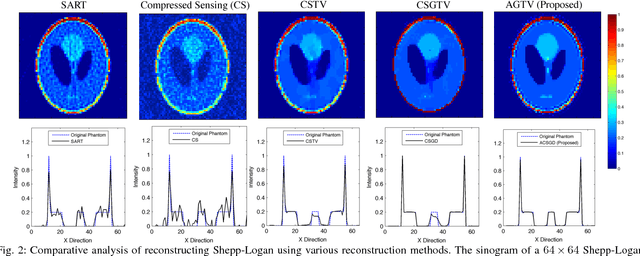
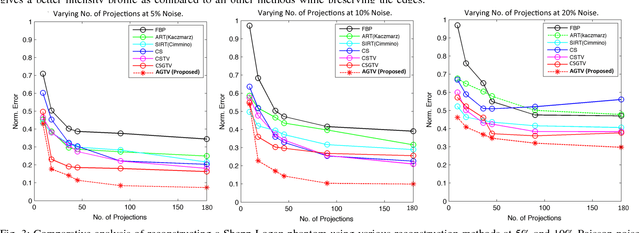
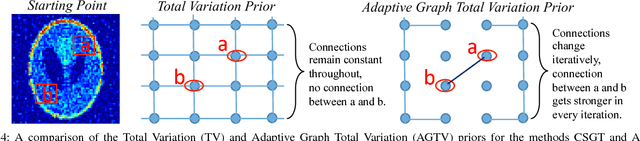
Sparsity exploiting image reconstruction (SER) methods have been extensively used with Total Variation (TV) regularization for tomographic reconstructions. Local TV methods fail to preserve texture details and often create additional artefacts due to over-smoothing. Non-Local TV (NLTV) methods have been proposed as a solution to this but they either lack continuous updates due to computational constraints or limit the locality to a small region. In this paper, we propose Adaptive Graph-based TV (AGTV). The proposed method goes beyond spatial similarity between different regions of an image being reconstructed by establishing a connection between similar regions in the entire image regardless of spatial distance. As compared to NLTV the proposed method is computationally efficient and involves updating the graph prior during every iteration making the connection between similar regions stronger. Moreover, it promotes sparsity in the wavelet and graph gradient domains. Since TV is a special case of graph TV the proposed method can also be seen as a generalization of SER and TV methods.

2D Discrete Fourier Transform with Simultaneous Edge Artifact Removal for Real-Time Applications

Two-Dimensional (2D) Discrete Fourier Transform (DFT) is a basic and computationally intensive algorithm, with a vast variety of applications. 2D images are, in general, non-periodic, but are assumed to be periodic while calculating their DFTs. This leads to cross-shaped artifacts in the frequency domain due to spectral leakage. These artifacts can have critical consequences if the DFTs are being used for further processing. In this paper we present a novel FPGA-based design to calculate high-throughput 2D DFTs with simultaneous edge artifact removal. Standard approaches for removing these artifacts using apodization functions or mirroring, either involve removing critical frequencies or a surge in computation by increasing image size. We use a periodic-plus-smooth decomposition based artifact removal algorithm optimized for FPGA implementation, while still achieving real-time ($\ge$23 frames per second) performance for a 512$\times$512 size image stream. Our optimization approach leads to a significant decrease in external memory utilization thereby avoiding memory conflicts and simplifies the design. We have tested our design on a PXIe based Xilinx Kintex 7 FPGA system communicating with a host PC which gives us the advantage to further expand the design for industrial applications.

Graph Based Sinogram Denoising for Tomographic Reconstructions

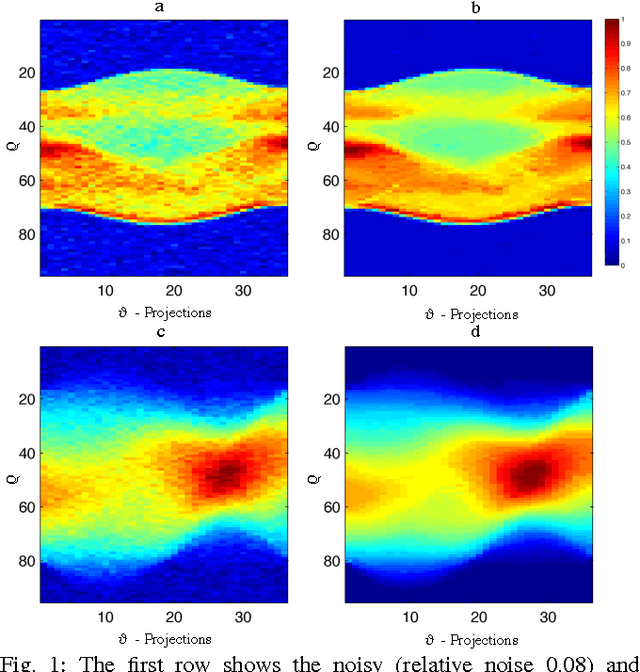
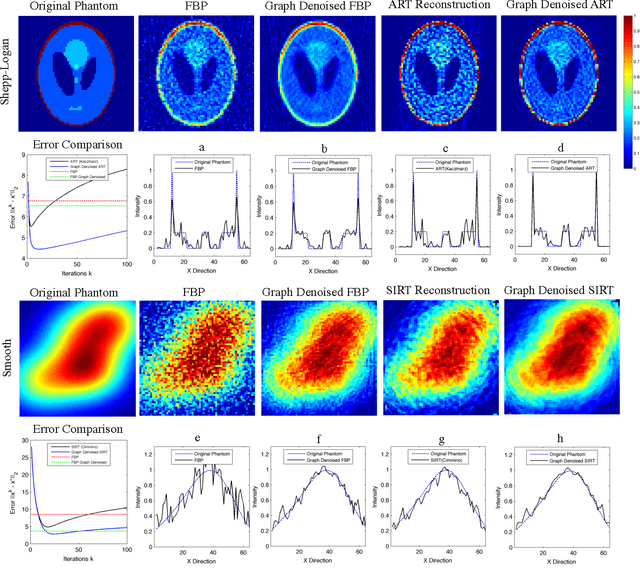
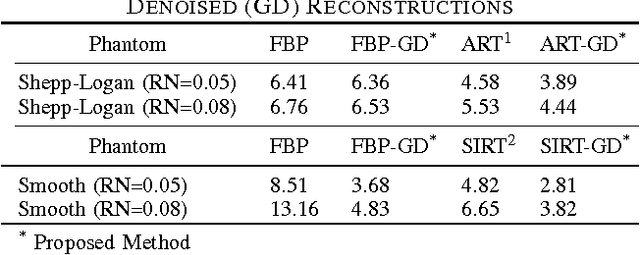
Limited data and low dose constraints are common problems in a variety of tomographic reconstruction paradigms which lead to noisy and incomplete data. Over the past few years sinogram denoising has become an essential pre-processing step for low dose Computed Tomographic (CT) reconstructions. We propose a novel sinogram denoising algorithm inspired by the modern field of signal processing on graphs. Graph based methods often perform better than standard filtering operations since they can exploit the signal structure. This makes the sinogram an ideal candidate for graph based denoising since it generally has a piecewise smooth structure. We test our method with a variety of phantoms and different reconstruction methods. Our numerical study shows that the proposed algorithm improves the performance of analytical filtered back-projection (FBP) and iterative methods ART (Kaczmarz) and SIRT (Cimmino).We observed that graph denoised sinogram always minimizes the error measure and improves the accuracy of the solution as compared to regular reconstructions.