Fidelity-based Probabilistic Q-learning for Control of Quantum Systems

The balance between exploration and exploitation is a key problem for reinforcement learning methods, especially for Q-learning. In this paper, a fidelity-based probabilistic Q-learning (FPQL) approach is presented to naturally solve this problem and applied for learning control of quantum systems. In this approach, fidelity is adopted to help direct the learning process and the probability of each action to be selected at a certain state is updated iteratively along with the learning process, which leads to a natural exploration strategy instead of a pointed one with configured parameters. A probabilistic Q-learning (PQL) algorithm is first presented to demonstrate the basic idea of probabilistic action selection. Then the FPQL algorithm is presented for learning control of quantum systems. Two examples (a spin- 1/2 system and a lamda-type atomic system) are demonstrated to test the performance of the FPQL algorithm. The results show that FPQL algorithms attain a better balance between exploration and exploitation, and can also avoid local optimal policies and accelerate the learning process.

Quantum reinforcement learning

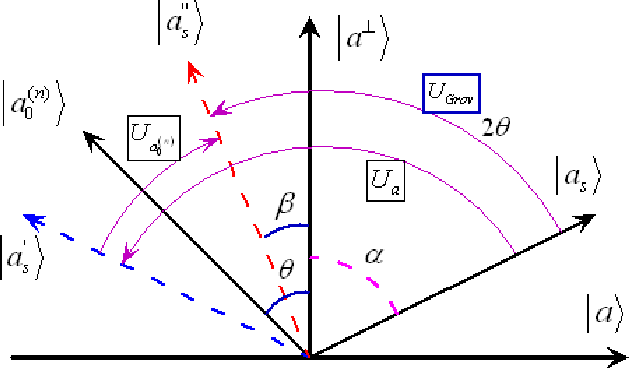
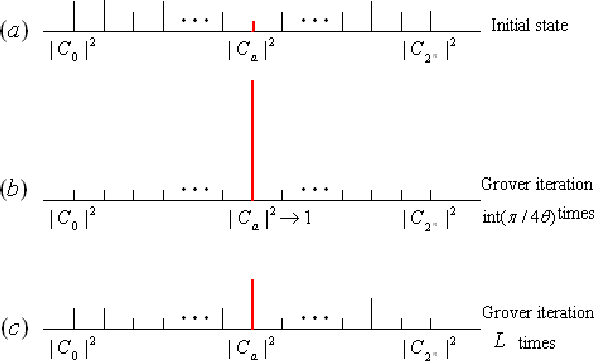
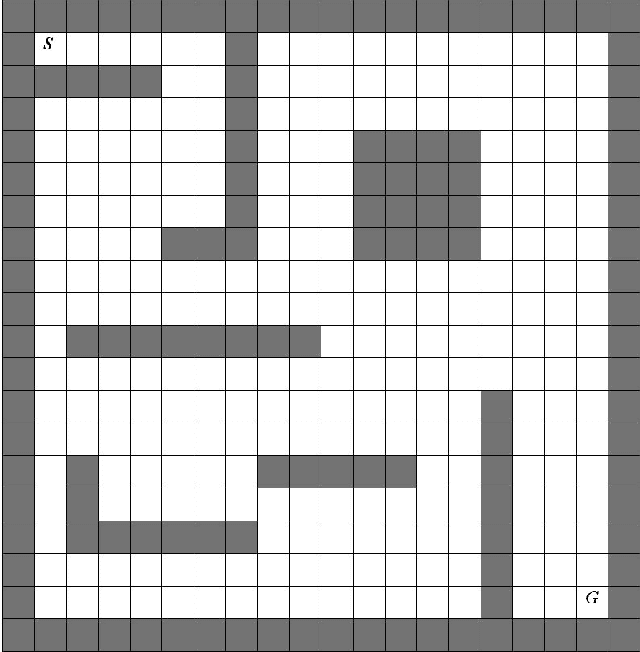
The key approaches for machine learning, especially learning in unknown probabilistic environments are new representations and computation mechanisms. In this paper, a novel quantum reinforcement learning (QRL) method is proposed by combining quantum theory and reinforcement learning (RL). Inspired by the state superposition principle and quantum parallelism, a framework of value updating algorithm is introduced. The state (action) in traditional RL is identified as the eigen state (eigen action) in QRL. The state (action) set can be represented with a quantum superposition state and the eigen state (eigen action) can be obtained by randomly observing the simulated quantum state according to the collapse postulate of quantum measurement. The probability of the eigen action is determined by the probability amplitude, which is parallelly updated according to rewards. Some related characteristics of QRL such as convergence, optimality and balancing between exploration and exploitation are also analyzed, which shows that this approach makes a good tradeoff between exploration and exploitation using the probability amplitude and can speed up learning through the quantum parallelism. To evaluate the performance and practicability of QRL, several simulated experiments are given and the results demonstrate the effectiveness and superiority of QRL algorithm for some complex problems. The present work is also an effective exploration on the application of quantum computation to artificial intelligence.