Guiding a Diffusion Model with a Bad Version of Itself

The primary axes of interest in image-generating diffusion models are image quality, the amount of variation in the results, and how well the results align with a given condition, e.g., a class label or a text prompt. The popular classifier-free guidance approach uses an unconditional model to guide a conditional model, leading to simultaneously better prompt alignment and higher-quality images at the cost of reduced variation. These effects seem inherently entangled, and thus hard to control. We make the surprising observation that it is possible to obtain disentangled control over image quality without compromising the amount of variation by guiding generation using a smaller, less-trained version of the model itself rather than an unconditional model. This leads to significant improvements in ImageNet generation, setting record FIDs of 1.01 for 64x64 and 1.25 for 512x512, using publicly available networks. Furthermore, the method is also applicable to unconditional diffusion models, drastically improving their quality.

Applying Guidance in a Limited Interval Improves Sample and Distribution Quality in Diffusion Models

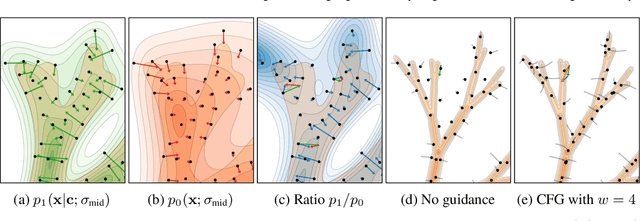
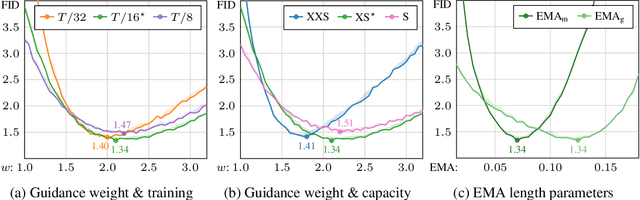
Guidance is a crucial technique for extracting the best performance out of image-generating diffusion models. Traditionally, a constant guidance weight has been applied throughout the sampling chain of an image. We show that guidance is clearly harmful toward the beginning of the chain (high noise levels), largely unnecessary toward the end (low noise levels), and only beneficial in the middle. We thus restrict it to a specific range of noise levels, improving both the inference speed and result quality. This limited guidance interval improves the record FID in ImageNet-512 significantly, from 1.81 to 1.40. We show that it is quantitatively and qualitatively beneficial across different sampler parameters, network architectures, and datasets, including the large-scale setting of Stable Diffusion XL. We thus suggest exposing the guidance interval as a hyperparameter in all diffusion models that use guidance.

Disentangling Random and Cyclic Effects in Time-Lapse Sequences

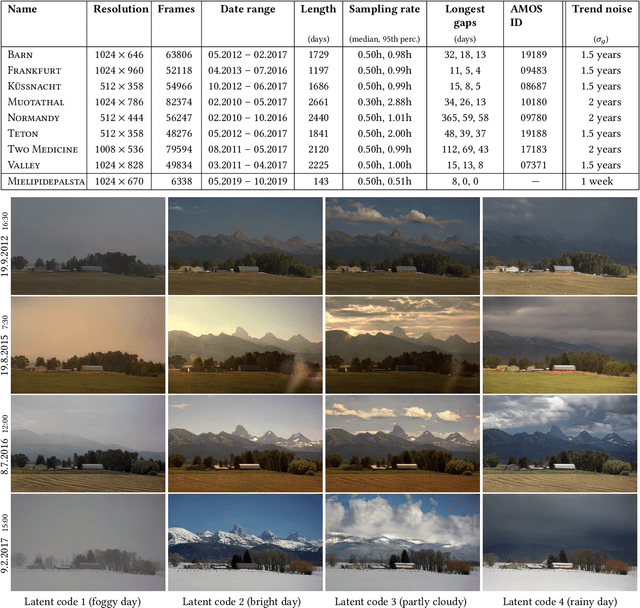
Time-lapse image sequences offer visually compelling insights into dynamic processes that are too slow to observe in real time. However, playing a long time-lapse sequence back as a video often results in distracting flicker due to random effects, such as weather, as well as cyclic effects, such as the day-night cycle. We introduce the problem of disentangling time-lapse sequences in a way that allows separate, after-the-fact control of overall trends, cyclic effects, and random effects in the images, and describe a technique based on data-driven generative models that achieves this goal. This enables us to "re-render" the sequences in ways that would not be possible with the input images alone. For example, we can stabilize a long sequence to focus on plant growth over many months, under selectable, consistent weather. Our approach is based on Generative Adversarial Networks (GAN) that are conditioned with the time coordinate of the time-lapse sequence. Our architecture and training procedure are designed so that the networks learn to model random variations, such as weather, using the GAN's latent space, and to disentangle overall trends and cyclic variations by feeding the conditioning time label to the model using Fourier features with specific frequencies. We show that our models are robust to defects in the training data, enabling us to amend some of the practical difficulties in capturing long time-lapse sequences, such as temporary occlusions, uneven frame spacing, and missing frames.

The Role of ImageNet Classes in Fréchet Inception Distance

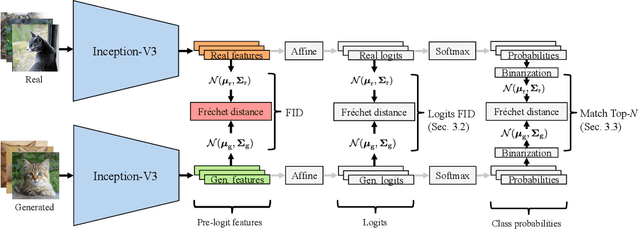
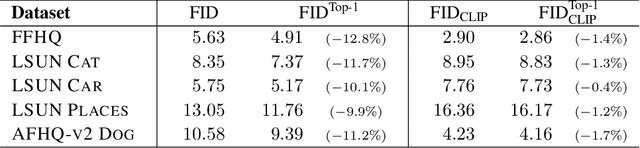
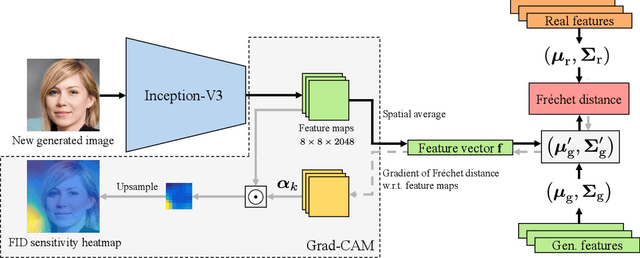
Fr\'echet Inception Distance (FID) is a metric for quantifying the distance between two distributions of images. Given its status as a standard yardstick for ranking models in data-driven generative modeling research, it seems important that the distance is computed from general, "vision-related" features. But is it? We observe that FID is essentially a distance between sets of ImageNet class probabilities. We trace the reason to the fact that the standard feature space, the penultimate "pre-logit" layer of a particular Inception-V3 classifier network, is only one affine transform away from the logits, i.e., ImageNet classes, and thus, the features are necessarily highly specialized to them. This has unintuitive consequences for the metric's sensitivity. For example, when evaluating a model for human faces, we observe that, on average, FID is actually very insensitive to the facial region, and that the probabilities of classes like "bow tie" or "seat belt" play a much larger role. Further, we show that FID can be significantly reduced -- without actually improving the quality of results -- by an attack that first generates a slightly larger set of candidates, and then chooses a subset that happens to match the histogram of such "fringe features" in the real data. We then demonstrate that this observation has practical relevance in case of ImageNet pre-training of GANs, where a part of the observed FID improvement turns out not to be real. Our results suggest caution against over-interpreting FID improvements, and underline the need for distribution metrics that are more perceptually uniform.

Improved Precision and Recall Metric for Assessing Generative Models

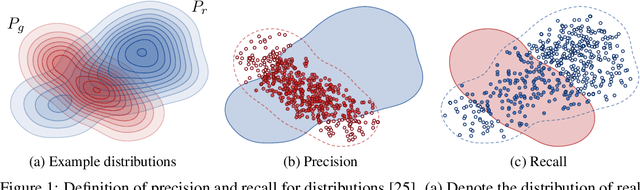
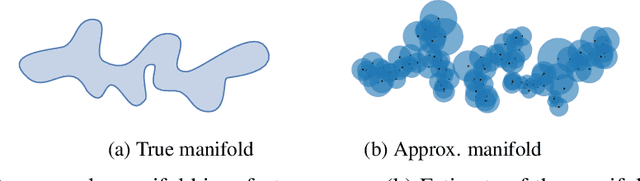
The ability to evaluate the performance of a computational model is a vital requirement for driving algorithm research. This is often particularly difficult for generative models such as generative adversarial networks (GAN) that model a data manifold only specified indirectly by a finite set of training examples. In the common case of image data, the samples live in a high-dimensional embedding space with little structure to help assessing either the overall quality of samples or the coverage of the underlying manifold. We present an evaluation metric with the ability to separately and reliably measure both of these aspects in image generation tasks by forming explicit non-parametric representations of the manifolds of real and generated data. We demonstrate the effectiveness of our metric in StyleGAN and BigGAN by providing several illustrative examples where existing metrics yield uninformative or contradictory results. Furthermore, we analyze multiple design variants of StyleGAN to better understand the relationships between the model architecture, training methods, and the properties of the resulting sample distribution. In the process, we identify new variants that improve the state-of-the-art. We also perform the first principled analysis of truncation methods and identify an improved method. Finally, we extend our metric to estimate the perceptual quality of individual samples, and use this to study latent space interpolations.