Decoder Decomposition for the Analysis of the Latent Space of Nonlinear Autoencoders With Wind-Tunnel Experimental Data

Turbulent flows are chaotic and multi-scale dynamical systems, which have large numbers of degrees of freedom. Turbulent flows, however, can be modelled with a smaller number of degrees of freedom when using the appropriate coordinate system, which is the goal of dimensionality reduction via nonlinear autoencoders. Autoencoders are expressive tools, but they are difficult to interpret. The goal of this paper is to propose a method to aid the interpretability of autoencoders. This is the decoder decomposition. First, we propose the decoder decomposition, which is a post-processing method to connect the latent variables to the coherent structures of flows. Second, we apply the decoder decomposition to analyse the latent space of synthetic data of a two-dimensional unsteady wake past a cylinder. We find that the dimension of latent space has a significant impact on the interpretability of autoencoders. We identify the physical and spurious latent variables. Third, we apply the decoder decomposition to the latent space of wind-tunnel experimental data of a three-dimensional turbulent wake past a bluff body. We show that the reconstruction error is a function of both the latent space dimension and the decoder size, which are correlated. Finally, we apply the decoder decomposition to rank and select latent variables based on the coherent structures that they represent. This is useful to filter unwanted or spurious latent variables, or to pinpoint specific coherent structures of interest. The ability to rank and select latent variables will help users design and interpret nonlinear autoencoders.

A machine learning approach to the prediction of heat-transfer coefficients in micro-channels

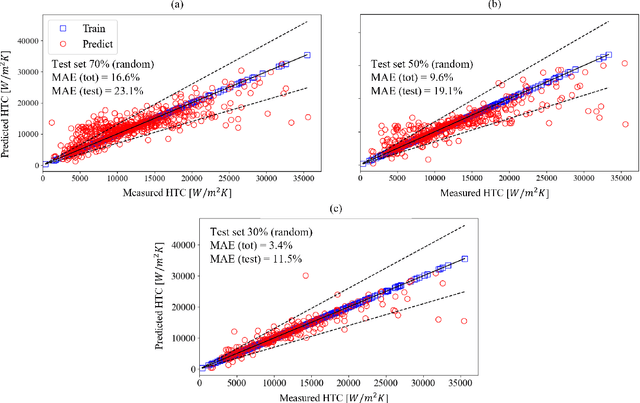
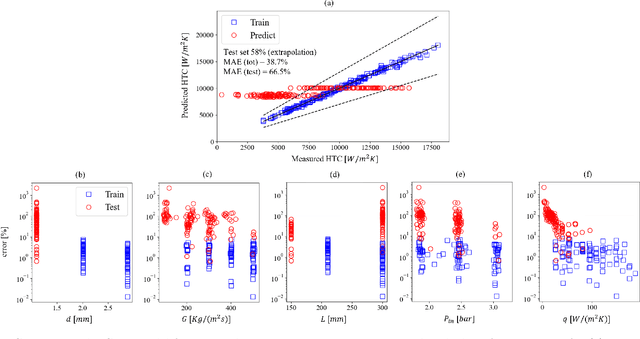
The accurate prediction of the two-phase heat transfer coefficient (HTC) as a function of working fluids, channel geometries and process conditions is key to the optimal design and operation of compact heat exchangers. Advances in artificial intelligence research have recently boosted the application of machine learning (ML) algorithms to obtain data-driven surrogate models for the HTC. For most supervised learning algorithms, the task is that of a nonlinear regression problem. Despite the fact that these models have been proven capable of outperforming traditional empirical correlations, they have key limitations such as overfitting the data, the lack of uncertainty estimation, and interpretability of the results. To address these limitations, in this paper, we use a multi-output Gaussian process regression (GPR) to estimate the HTC in microchannels as a function of the mass flow rate, heat flux, system pressure and channel diameter and length. The model is trained using the Brunel Two-Phase Flow database of high-fidelity experimental data. The advantages of GPR are data efficiency, the small number of hyperparameters to be trained (typically of the same order of the number of input dimensions), and the automatic trade-off between data fit and model complexity guaranteed by the maximization of the marginal likelihood (Bayesian approach). Our paper proposes research directions to improve the performance of the GPR-based model in extrapolation.

Data assimilation in a nonlinear time-delayed dynamical system

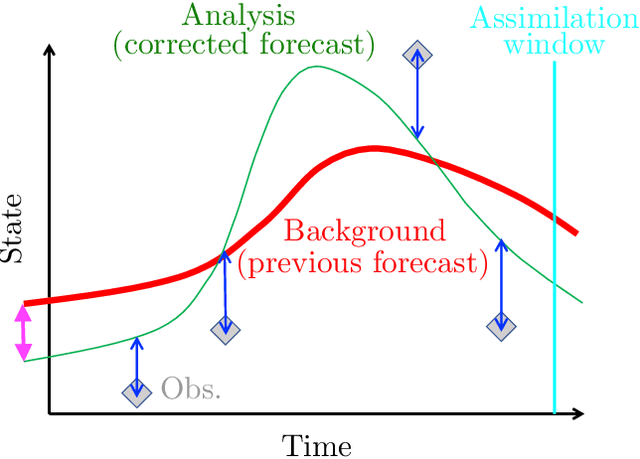
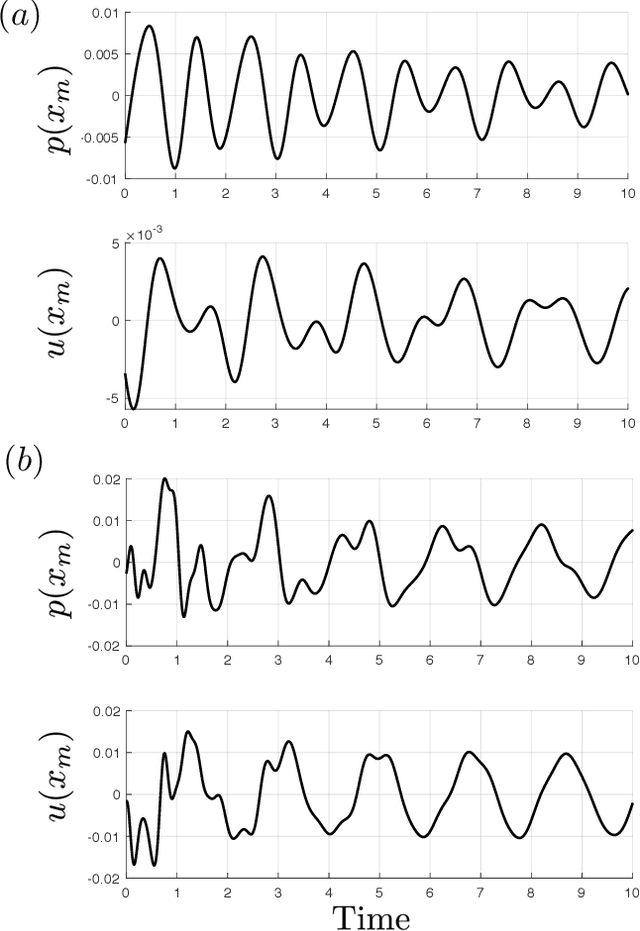
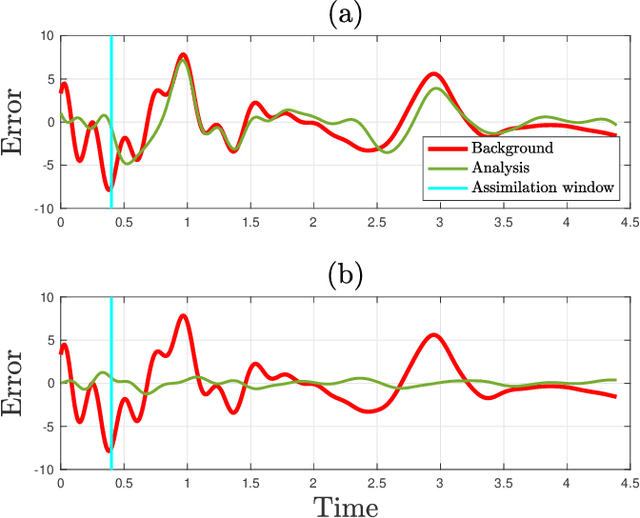
When the heat released by a flame is sufficiently in phase with the acoustic pressure, a self-excited thermoacoustic oscillation can arise. These nonlinear oscillations are one of the biggest challenges faced in the design of safe and reliable gas turbines and rocket motors. In the worst-case scenario, uncontrolled thermoacoustic oscillations can shake an engine apart. Reduced-order thermoacoustic models, which are nonlinear and time-delayed, can only qualitatively predict thermoacoustic oscillations. To make reduced-order models quantitatively predictive, we develop a data assimilation framework for state estimation. We numerically estimate the most likely nonlinear state of a Galerkin-discretized time delayed model of a horizontal Rijke tube, which is a prototypical combustor. Data assimilation is an optimal blending of observations with previous state estimates (background) to produce optimal initial conditions. A cost functional is defined to measure the statistical distance between the model output and the measurements from experiments; and the distance between the initial conditions and the background knowledge. Its minimum corresponds to the optimal state, which is computed by Lagrangian optimization with the aid of adjoint equations. We study the influence of the number of Galerkin modes, which are the natural acoustic modes of the duct, with which the model is discretized. We show that decomposing the measured pressure signal in a finite number of modes is an effective way to enhance state estimation, especially when nonlinear modal interactions occur during the assimilation window. This work represents the first application of data assimilation to nonlinear thermoacoustics, which opens up new possibilities for real-time calibration of reduced-order models with experimental measurements.