A machine learning approach to the prediction of heat-transfer coefficients in micro-channels

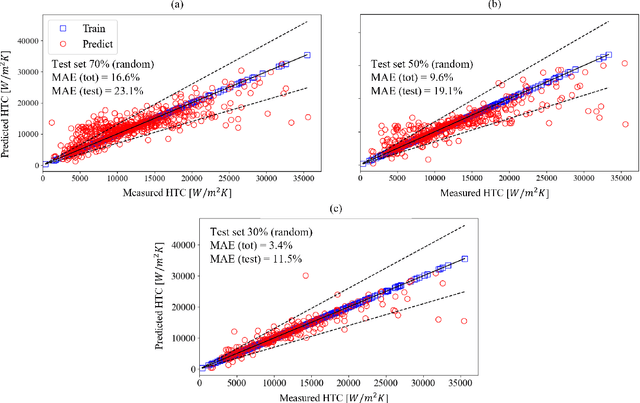
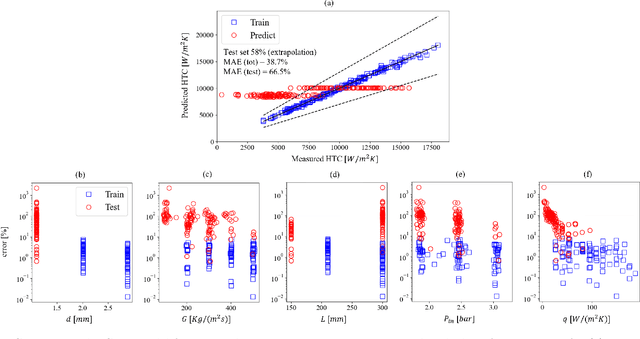
The accurate prediction of the two-phase heat transfer coefficient (HTC) as a function of working fluids, channel geometries and process conditions is key to the optimal design and operation of compact heat exchangers. Advances in artificial intelligence research have recently boosted the application of machine learning (ML) algorithms to obtain data-driven surrogate models for the HTC. For most supervised learning algorithms, the task is that of a nonlinear regression problem. Despite the fact that these models have been proven capable of outperforming traditional empirical correlations, they have key limitations such as overfitting the data, the lack of uncertainty estimation, and interpretability of the results. To address these limitations, in this paper, we use a multi-output Gaussian process regression (GPR) to estimate the HTC in microchannels as a function of the mass flow rate, heat flux, system pressure and channel diameter and length. The model is trained using the Brunel Two-Phase Flow database of high-fidelity experimental data. The advantages of GPR are data efficiency, the small number of hyperparameters to be trained (typically of the same order of the number of input dimensions), and the automatic trade-off between data fit and model complexity guaranteed by the maximization of the marginal likelihood (Bayesian approach). Our paper proposes research directions to improve the performance of the GPR-based model in extrapolation.