Reconstructing unsteady flows from sparse, noisy measurements with a physics-constrained convolutional neural network

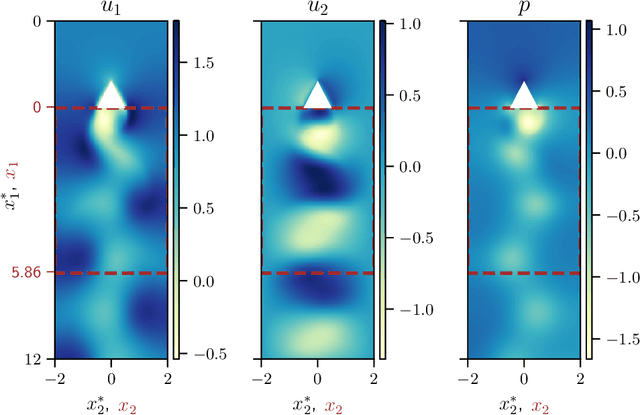
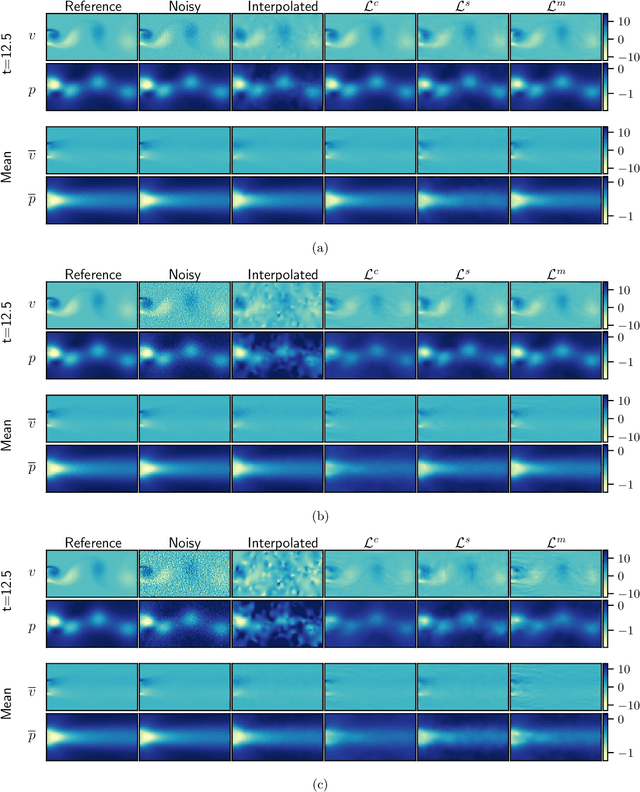
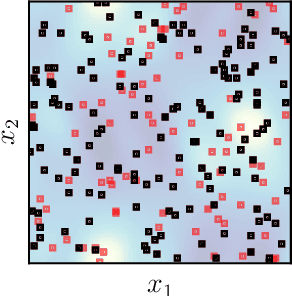
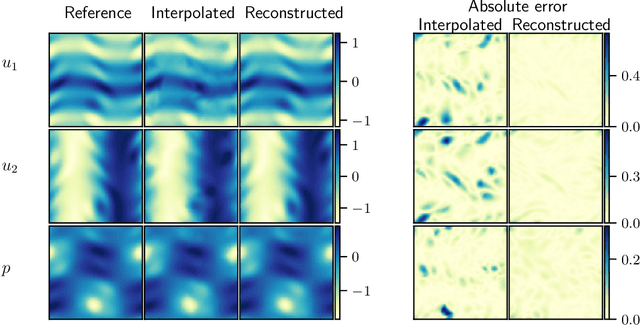
Data from fluid flow measurements are typically sparse, noisy, and heterogeneous, often from mixed pressure and velocity measurements, resulting in incomplete datasets. In this paper, we develop a physics-constrained convolutional neural network, which is a deterministic tool, to reconstruct the full flow field from incomplete data. We explore three loss functions, both from machine learning literature and newly proposed: (i) the softly-constrained loss, which allows the prediction to take any value; (ii) the snapshot-enforced loss, which constrains the prediction at the sensor locations; and (iii) the mean-enforced loss, which constrains the mean of the prediction at the sensor locations. The proposed methods do not require the full flow field during training, making it suitable for reconstruction from incomplete data. We apply the method to reconstruct a laminar wake of a bluff body and a turbulent Kolmogorov flow. First, we assume that measurements are not noisy and reconstruct both the laminar wake and the Kolmogorov flow from sensors located at fewer than 1% of all grid points. The snapshot-enforced loss reduces the reconstruction error of the Kolmogorov flow by approximately 25% compared to the softly-constrained loss. Second, we assume that measurements are noisy and propose the mean-enforced loss to reconstruct the laminar wake and the Kolmogorov flow at three different signal-to-noise ratios. We find that, across the ratios tested, the loss functions with harder constraints are more robust to both the random initialization of the networks and the noise levels in the measurements. At high noise levels, the mean-enforced loss can recover the instantaneous snapshots accurately, making it the suitable choice when reconstructing flows from data corrupted with an unknown amount of noise. The proposed method opens opportunities for physical flow reconstruction from sparse, noisy data.

Decoder Decomposition for the Analysis of the Latent Space of Nonlinear Autoencoders With Wind-Tunnel Experimental Data

Turbulent flows are chaotic and multi-scale dynamical systems, which have large numbers of degrees of freedom. Turbulent flows, however, can be modelled with a smaller number of degrees of freedom when using the appropriate coordinate system, which is the goal of dimensionality reduction via nonlinear autoencoders. Autoencoders are expressive tools, but they are difficult to interpret. The goal of this paper is to propose a method to aid the interpretability of autoencoders. This is the decoder decomposition. First, we propose the decoder decomposition, which is a post-processing method to connect the latent variables to the coherent structures of flows. Second, we apply the decoder decomposition to analyse the latent space of synthetic data of a two-dimensional unsteady wake past a cylinder. We find that the dimension of latent space has a significant impact on the interpretability of autoencoders. We identify the physical and spurious latent variables. Third, we apply the decoder decomposition to the latent space of wind-tunnel experimental data of a three-dimensional turbulent wake past a bluff body. We show that the reconstruction error is a function of both the latent space dimension and the decoder size, which are correlated. Finally, we apply the decoder decomposition to rank and select latent variables based on the coherent structures that they represent. This is useful to filter unwanted or spurious latent variables, or to pinpoint specific coherent structures of interest. The ability to rank and select latent variables will help users design and interpret nonlinear autoencoders.