Tsimboy Olga
Denoising Score Matching with Random Fourier Features
Jan 13, 2021
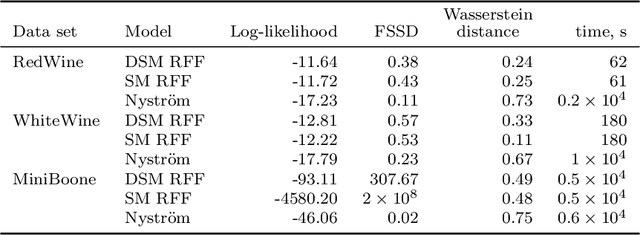
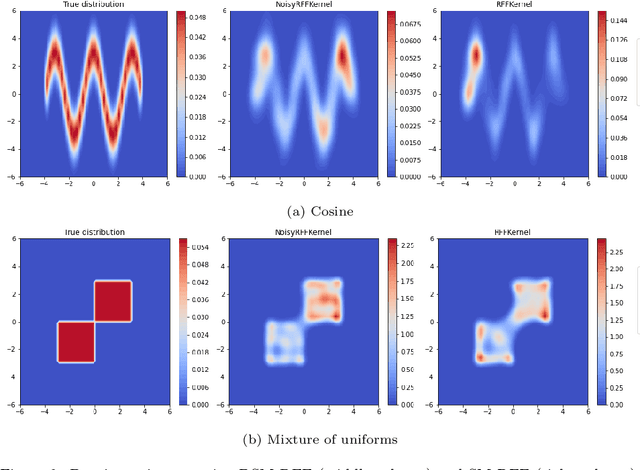
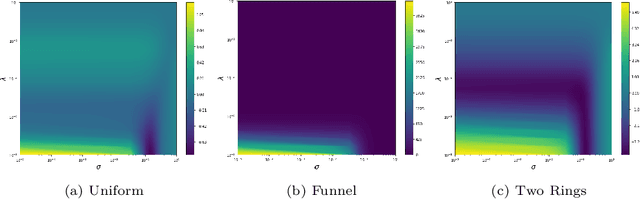
Abstract:The density estimation is one of the core problems in statistics. Despite this, existing techniques like maximum likelihood estimation are computationally inefficient due to the intractability of the normalizing constant. For this reason an interest to score matching has increased being independent on the normalizing constant. However, such estimator is consistent only for distributions with the full space support. One of the approaches to make it consistent is to add noise to the input data which is called Denoising Score Matching. In this work we derive analytical expression for the Denoising Score matching using the Kernel Exponential Family as a model distribution. The usage of the kernel exponential family is motivated by the richness of this class of densities. To tackle the computational complexity we use Random Fourier Features based approximation of the kernel function. The analytical expression allows to drop additional regularization terms based on the higher-order derivatives as they are already implicitly included. Moreover, the obtained expression explicitly depends on the noise variance, so the validation loss can be straightforwardly used to tune the noise level. Along with benchmark experiments, the model was tested on various synthetic distributions to study the behaviour of the model in different cases. The empirical study shows comparable quality to the competing approaches, while the proposed method being computationally faster. The latter one enables scaling up to complex high-dimensional data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge