Interpreting and Improving Optimal Control Problems with Directional Corrections

Many robotics tasks, such as path planning or trajectory optimization, are formulated as optimal control problems (OCPs). The key to obtaining high performance lies in the design of the OCP's objective function. In practice, the objective function consists of a set of individual components that must be carefully modeled and traded off such that the OCP has the desired solution. It is often challenging to balance multiple components to achieve the desired solution and to understand, when the solution is undesired, the impact of individual cost components. In this paper, we present a framework addressing these challenges based on the concept of directional corrections. Specifically, given the solution to an OCP that is deemed undesirable, and access to an expert providing the direction of change that would increase the desirability of the solution, our method analyzes the individual cost components for their "consistency" with the provided directional correction. This information can be used to improve the OCP formulation, e.g., by increasing the weight of consistent cost components, or reducing the weight of - or even redesigning - inconsistent cost components. We also show that our framework can automatically tune parameters of the OCP to achieve consistency with a set of corrections.

Information Maximizing Exploration with a Latent Dynamics Model

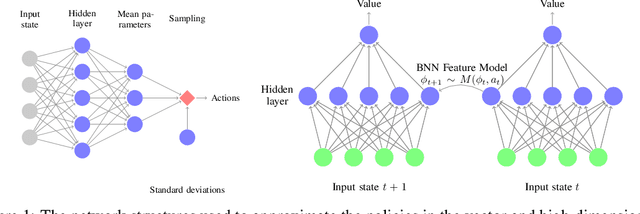
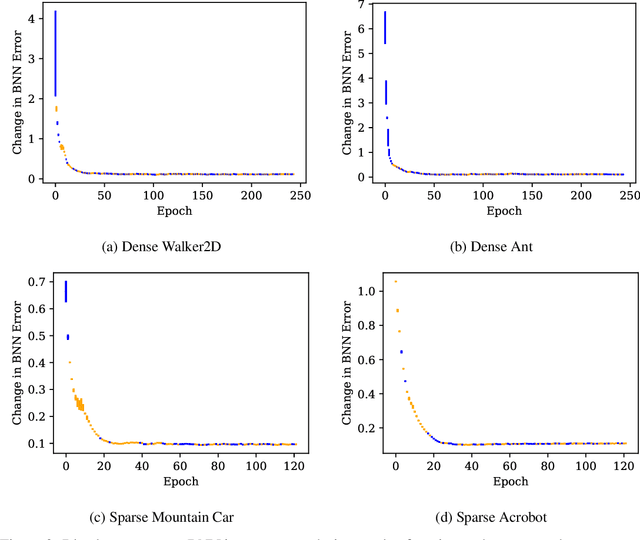
All reinforcement learning algorithms must handle the trade-off between exploration and exploitation. Many state-of-the-art deep reinforcement learning methods use noise in the action selection, such as Gaussian noise in policy gradient methods or $\epsilon$-greedy in Q-learning. While these methods are appealing due to their simplicity, they do not explore the state space in a methodical manner. We present an approach that uses a model to derive reward bonuses as a means of intrinsic motivation to improve model-free reinforcement learning. A key insight of our approach is that this dynamics model can be learned in the latent feature space of a value function, representing the dynamics of the agent and the environment. This method is both theoretically grounded and computationally advantageous, permitting the efficient use of Bayesian information-theoretic methods in high-dimensional state spaces. We evaluate our method on several continuous control tasks, focusing on improving exploration.