Hyperbolic Recommender Systems

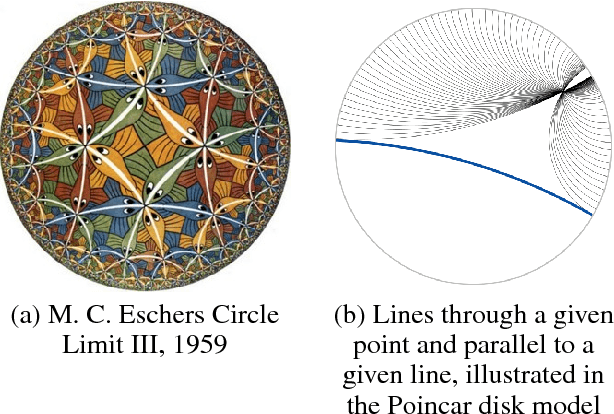
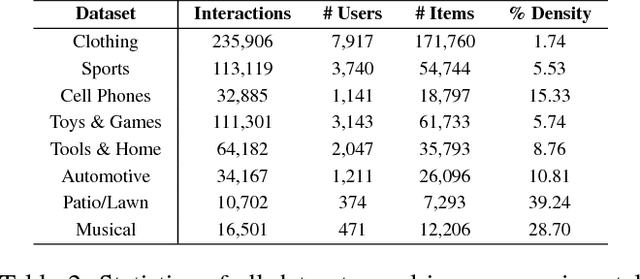
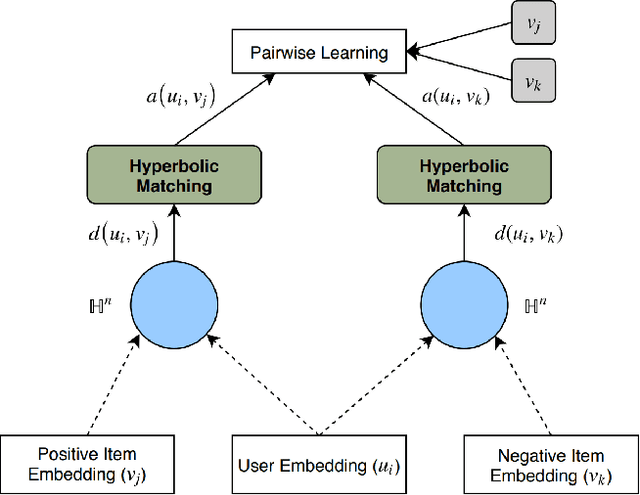
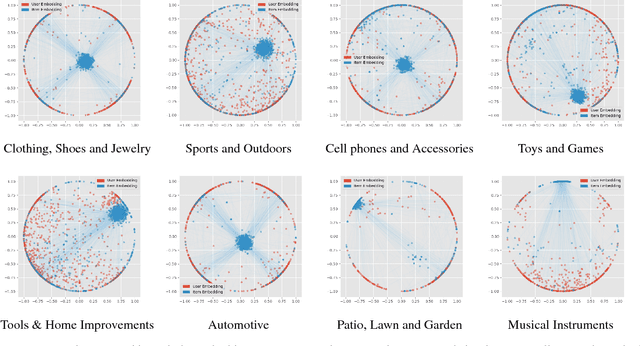
Many well-established recommender systems are based on representation learning in Euclidean space. In these models, matching functions such as the Euclidean distance or inner product are typically used for computing similarity scores between user and item embeddings. This paper investigates the notion of learning user and item representations in Hyperbolic space. In this paper, we argue that Hyperbolic space is more suitable for learning user-item embeddings in the recommendation domain. Unlike Euclidean spaces, Hyperbolic spaces are intrinsically equipped to handle hierarchical structure, encouraged by its property of exponentially increasing distances away from origin. We propose HyperBPR (Hyperbolic Bayesian Personalized Ranking), a conceptually simple but highly effective model for the task at hand. Our proposed HyperBPR not only outperforms their Euclidean counterparts, but also achieves state-of-the-art performance on multiple benchmark datasets, demonstrating the effectiveness of personalized recommendation in Hyperbolic space.

Attention-based Group Recommendation

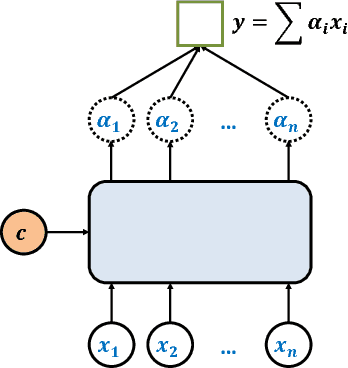
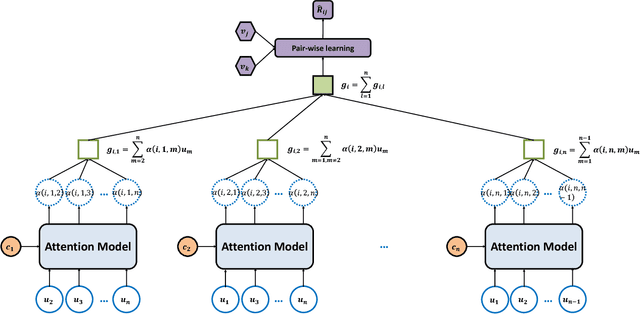
Group recommendation aims to recommend items for a group of users, e.g., recommending a restaurant for a group of colleagues. The group recommendation problem is challenging, in that a good model should understand the group decision making process appropriately: users are likely to follow decisions of only a few users, who are group's leaders or experts. To address this challenge, we propose using an attention mechanism to capture the impact of each user in a group. Specifically, our model learns the influence weight of each user in a group and recommends items to the group based on its members' weighted preferences. Moreover, our model can dynamically adjust the weight of each user across the groups; thus, the model provides a new and flexible method to model the complicated group decision making process, which differentiates us from other existing solutions. Through extensive experiments, it has demonstrated that our model significantly outperforms baseline methods for the group recommendation problem.