Hyperbolic Recommender Systems

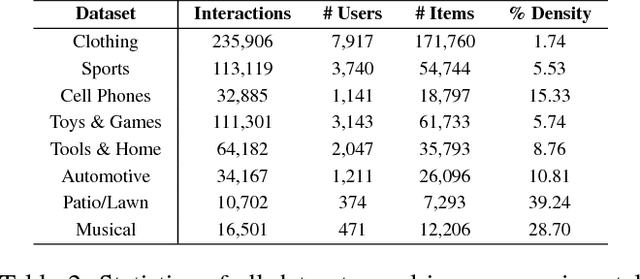
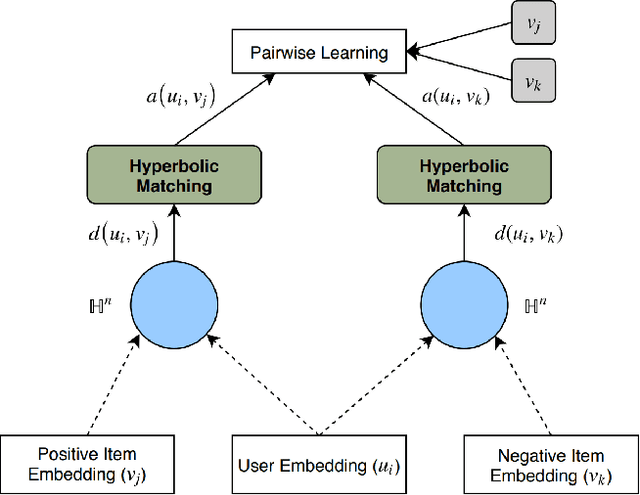
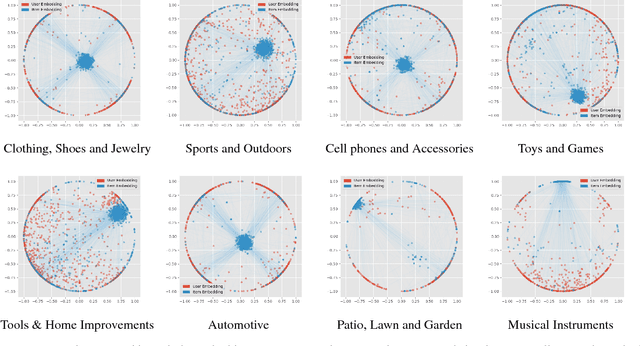
Many well-established recommender systems are based on representation learning in Euclidean space. In these models, matching functions such as the Euclidean distance or inner product are typically used for computing similarity scores between user and item embeddings. This paper investigates the notion of learning user and item representations in Hyperbolic space. In this paper, we argue that Hyperbolic space is more suitable for learning user-item embeddings in the recommendation domain. Unlike Euclidean spaces, Hyperbolic spaces are intrinsically equipped to handle hierarchical structure, encouraged by its property of exponentially increasing distances away from origin. We propose HyperBPR (Hyperbolic Bayesian Personalized Ranking), a conceptually simple but highly effective model for the task at hand. Our proposed HyperBPR not only outperforms their Euclidean counterparts, but also achieves state-of-the-art performance on multiple benchmark datasets, demonstrating the effectiveness of personalized recommendation in Hyperbolic space.