Sequential- and Parallel- Constrained Max-value Entropy Search via Information Lower Bound

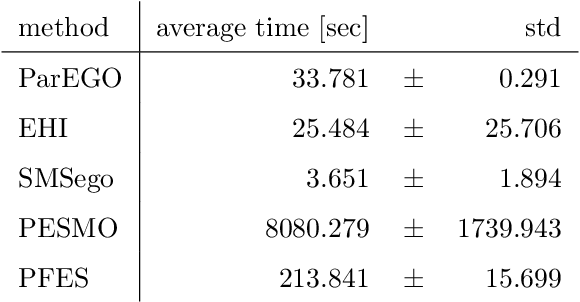
Recently, several Bayesian optimization (BO) methods have been extended to the expensive black-box optimization problem with unknown constraints, which is an important problem that appears frequently in practice. We focus on an information-theoretic approach called Max-value Entropy Search (MES) whose superior performance has been repeatedly shown in BO literature. Since existing MES-based constrained BO is restricted to only one constraint, we first extend it to multiple constraints, but we found that this approach can cause negative approximate values for the mutual information, which can result in unreasonable decisions. In this paper, we employ a different approximation strategy that is based on a lower bound of the mutual information, and propose a novel constrained BO method called Constrained Max-value Entropy Search via Information lower BOund (CMES-IBO). Our approximate mutual information derived from the lower bound has a simple closed-form that is guaranteed to be nonnegative, and we show that irrational behavior caused by the negative value can be avoided. Furthermore, by using conditional mutual information, we extend our methods to the parallel setting in which multiple queries can be issued simultaneously. Finally, we demonstrate the effectiveness of our proposed methods by benchmark functions and real-world applications to materials science.

Multi-objective Bayesian Optimization using Pareto-frontier Entropy

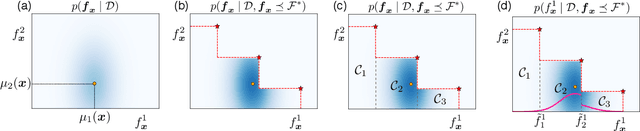
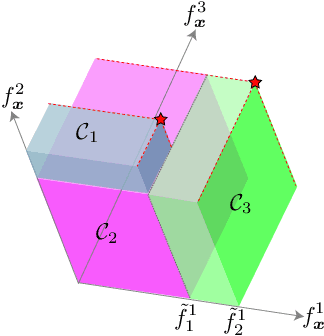
We propose Pareto-frontier entropy search (PFES) for multi-objective Bayesian optimization (MBO). Unlike the existing entropy search for MBO which considers the entropy of the input space, we define the entropy of Pareto-frontier in the output space. By using a sampled Pareto-frontier from the current model, PFES provides a simple formula for directly evaluating the entropy. Besides the usual MBO setting, in which all the objectives are simultaneously observed, we also consider the "decoupled" setting, in which the objective functions can be observed separately. PFES can easily derive an acquisition function for the decoupled setting through the entropy of the marginal density for each output variable. For the both settings, by conditioning on the sampled Pareto-frontier, dependence among different objectives arises in the entropy evaluation. PFES can incorporate this dependency into the acquisition function, while the existing information-based MBO employs an independent Gaussian approximation. Our numerical experiments show effectiveness of PFES through synthetic functions and real-world datasets from materials science.