A Unified Framework for Neural Computation and Learning Over Time

This paper proposes Hamiltonian Learning, a novel unified framework for learning with neural networks "over time", i.e., from a possibly infinite stream of data, in an online manner, without having access to future information. Existing works focus on the simplified setting in which the stream has a known finite length or is segmented into smaller sequences, leveraging well-established learning strategies from statistical machine learning. In this paper, the problem of learning over time is rethought from scratch, leveraging tools from optimal control theory, which yield a unifying view of the temporal dynamics of neural computations and learning. Hamiltonian Learning is based on differential equations that: (i) can be integrated without the need of external software solvers; (ii) generalize the well-established notion of gradient-based learning in feed-forward and recurrent networks; (iii) open to novel perspectives. The proposed framework is showcased by experimentally proving how it can recover gradient-based learning, comparing it to out-of-the box optimizers, and describing how it is flexible enough to switch from fully-local to partially/non-local computational schemes, possibly distributed over multiple devices, and BackPropagation without storing activations. Hamiltonian Learning is easy to implement and can help researches approach in a principled and innovative manner the problem of learning over time.

On the Resurgence of Recurrent Models for Long Sequences -- Survey and Research Opportunities in the Transformer Era

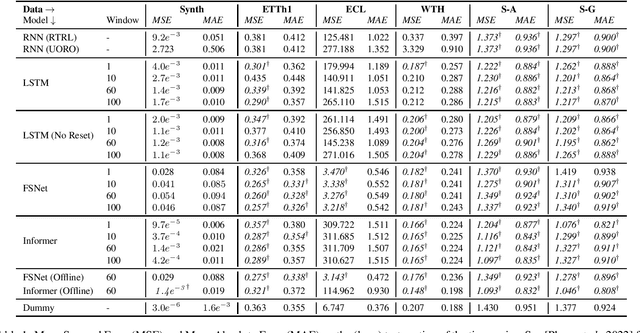
A longstanding challenge for the Machine Learning community is the one of developing models that are capable of processing and learning from very long sequences of data. The outstanding results of Transformers-based networks (e.g., Large Language Models) promotes the idea of parallel attention as the key to succeed in such a challenge, obfuscating the role of classic sequential processing of Recurrent Models. However, in the last few years, researchers who were concerned by the quadratic complexity of self-attention have been proposing a novel wave of neural models, which gets the best from the two worlds, i.e., Transformers and Recurrent Nets. Meanwhile, Deep Space-State Models emerged as robust approaches to function approximation over time, thus opening a new perspective in learning from sequential data, followed by many people in the field and exploited to implement a special class of (linear) Recurrent Neural Networks. This survey is aimed at providing an overview of these trends framed under the unifying umbrella of Recurrence. Moreover, it emphasizes novel research opportunities that become prominent when abandoning the idea of processing long sequences whose length is known-in-advance for the more realistic setting of potentially infinite-length sequences, thus intersecting the field of lifelong-online learning from streamed data.