Tomer Pelleg
HE-PEx: Efficient Machine Learning under Homomorphic Encryption using Pruning, Permutation and Expansion
Jul 07, 2022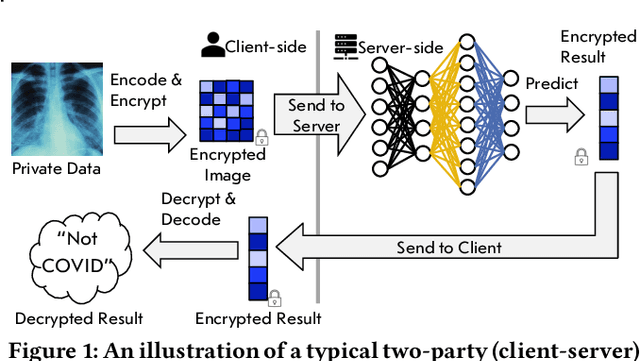

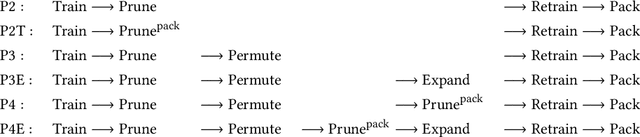
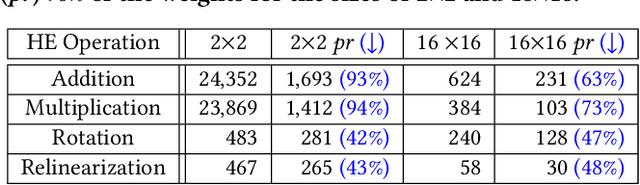
Abstract:Privacy-preserving neural network (NN) inference solutions have recently gained significant traction with several solutions that provide different latency-bandwidth trade-offs. Of these, many rely on homomorphic encryption (HE), a method of performing computations over encrypted data. However, HE operations even with state-of-the-art schemes are still considerably slow compared to their plaintext counterparts. Pruning the parameters of a NN model is a well-known approach to improving inference latency. However, pruning methods that are useful in the plaintext context may lend nearly negligible improvement in the HE case, as has also been demonstrated in recent work. In this work, we propose a novel set of pruning methods that reduce the latency and memory requirement, thus bringing the effectiveness of plaintext pruning methods to HE. Crucially, our proposal employs two key techniques, viz. permutation and expansion of the packed model weights, that enable pruning significantly more ciphertexts and recuperating most of the accuracy loss, respectively. We demonstrate the advantage of our method on fully connected layers where the weights are packed using a recently proposed packing technique called tile tensors, which allows executing deep NN inference in a non-interactive mode. We evaluate our methods on various autoencoder architectures and demonstrate that for a small mean-square reconstruction loss of 1.5*10^{-5} on MNIST, we reduce the memory requirement and latency of HE-enabled inference by 60%.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge