Hierarchical Clustering in $Λ$CDM Cosmologies via Persistence Energy

In this research, we investigate the structural evolution of the cosmic web, employing advanced methodologies from Topological Data Analysis. Our approach involves leveraging LITE, an innovative method from recent literature that embeds persistence diagrams into elements of vector spaces. Utilizing this methodology, we analyze three quintessential cosmic structures: clusters, filaments, and voids. A central discovery is the correlation between \textit{Persistence Energy} and redshift values, linking persistent homology with cosmic evolution and providing insights into the dynamics of cosmic structures.

Multi-Armed Bandits with Generalized Temporally-Partitioned Rewards

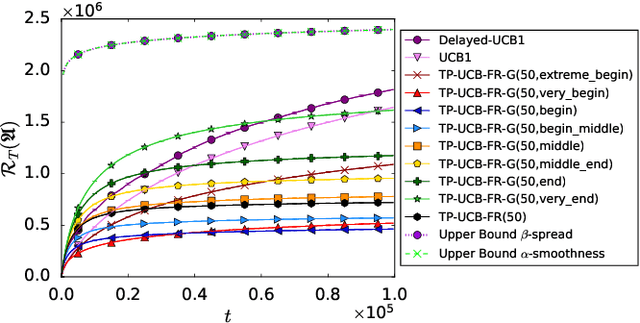
Decision-making problems of sequential nature, where decisions made in the past may have an impact on the future, are used to model many practically important applications. In some real-world applications, feedback about a decision is delayed and may arrive via partial rewards that are observed with different delays. Motivated by such scenarios, we propose a novel problem formulation called multi-armed bandits with generalized temporally-partitioned rewards. To formalize how feedback about a decision is partitioned across several time steps, we introduce $\beta$-spread property. We derive a lower bound on the performance of any uniformly efficient algorithm for the considered problem. Moreover, we provide an algorithm called TP-UCB-FR-G and prove an upper bound on its performance measure. In some scenarios, our upper bound improves upon the state of the art. We provide experimental results validating the proposed algorithm and our theoretical results.

Generalizing distribution of partial rewards for multi-armed bandits with temporally-partitioned rewards

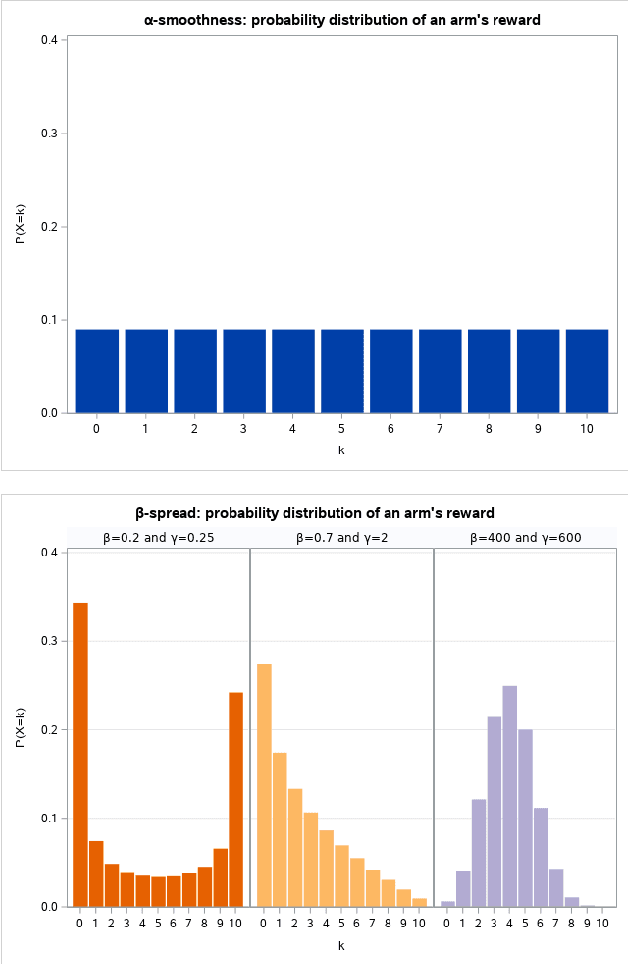
We investigate the Multi-Armed Bandit problem with Temporally-Partitioned Rewards (TP-MAB) setting in this paper. In the TP-MAB setting, an agent will receive subsets of the reward over multiple rounds rather than the entire reward for the arm all at once. In this paper, we introduce a general formulation of how an arm's cumulative reward is distributed across several rounds, called Beta-spread property. Such a generalization is needed to be able to handle partitioned rewards in which the maximum reward per round is not distributed uniformly across rounds. We derive a lower bound on the TP-MAB problem under the assumption that Beta-spread holds. Moreover, we provide an algorithm TP-UCB-FR-G, which uses the Beta-spread property to improve the regret upper bound in some scenarios. By generalizing how the cumulative reward is distributed, this setting is applicable in a broader range of applications.