Generalizing distribution of partial rewards for multi-armed bandits with temporally-partitioned rewards

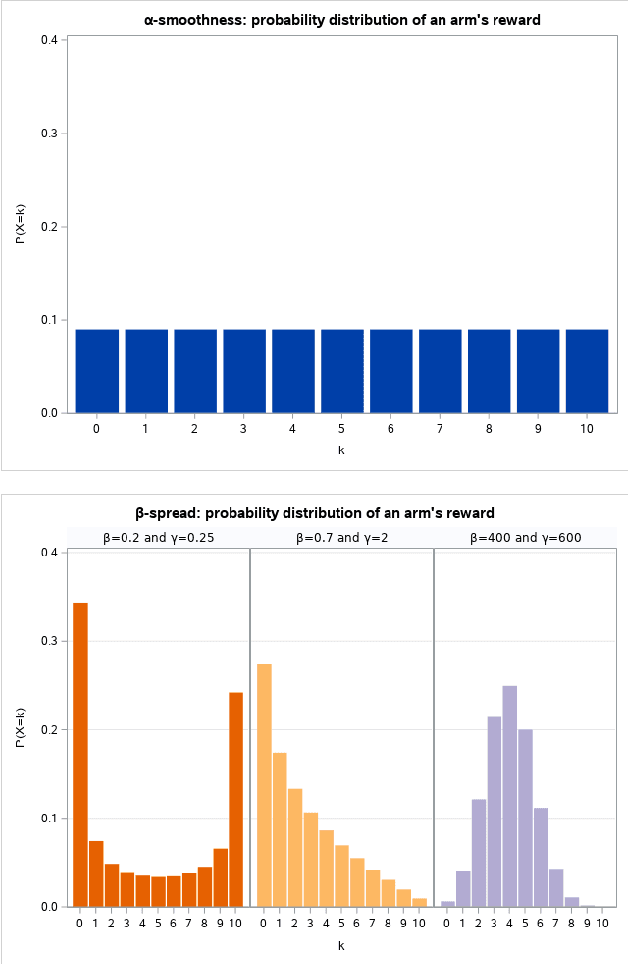
We investigate the Multi-Armed Bandit problem with Temporally-Partitioned Rewards (TP-MAB) setting in this paper. In the TP-MAB setting, an agent will receive subsets of the reward over multiple rounds rather than the entire reward for the arm all at once. In this paper, we introduce a general formulation of how an arm's cumulative reward is distributed across several rounds, called Beta-spread property. Such a generalization is needed to be able to handle partitioned rewards in which the maximum reward per round is not distributed uniformly across rounds. We derive a lower bound on the TP-MAB problem under the assumption that Beta-spread holds. Moreover, we provide an algorithm TP-UCB-FR-G, which uses the Beta-spread property to improve the regret upper bound in some scenarios. By generalizing how the cumulative reward is distributed, this setting is applicable in a broader range of applications.