Multi-Armed Bandits with Generalized Temporally-Partitioned Rewards

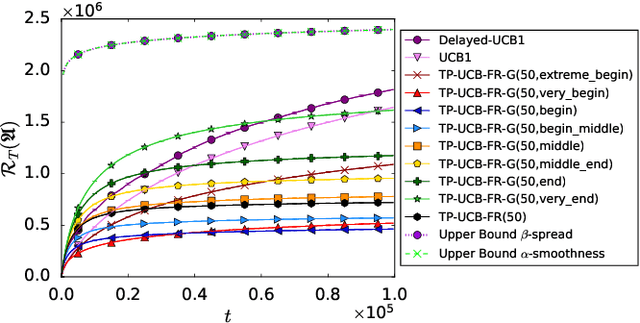
Decision-making problems of sequential nature, where decisions made in the past may have an impact on the future, are used to model many practically important applications. In some real-world applications, feedback about a decision is delayed and may arrive via partial rewards that are observed with different delays. Motivated by such scenarios, we propose a novel problem formulation called multi-armed bandits with generalized temporally-partitioned rewards. To formalize how feedback about a decision is partitioned across several time steps, we introduce $\beta$-spread property. We derive a lower bound on the performance of any uniformly efficient algorithm for the considered problem. Moreover, we provide an algorithm called TP-UCB-FR-G and prove an upper bound on its performance measure. In some scenarios, our upper bound improves upon the state of the art. We provide experimental results validating the proposed algorithm and our theoretical results.