Adaptive First- and Second-Order Algorithms for Large-Scale Machine Learning

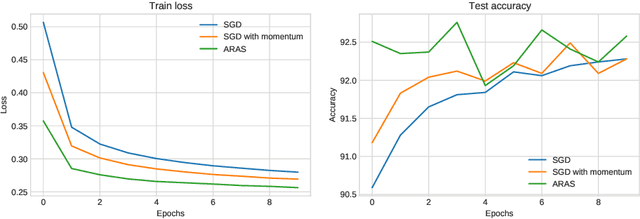
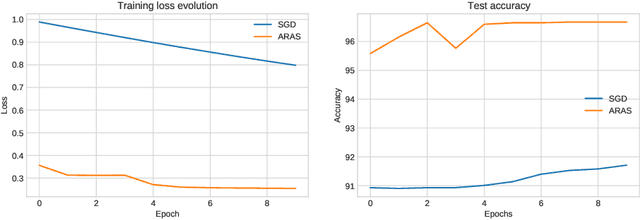
In this paper, we consider both first- and second-order techniques to address continuous optimization problems arising in machine learning. In the first-order case, we propose a framework of transition from deterministic or semi-deterministic to stochastic quadratic regularization methods. We leverage the two-phase nature of stochastic optimization to propose a novel first-order algorithm with adaptive sampling and adaptive step size. In the second-order case, we propose a novel stochastic damped L-BFGS method that improves on previous algorithms in the highly nonconvex context of deep learning. Both algorithms are evaluated on well-known deep learning datasets and exhibit promising performance.

Stochastic Damped L-BFGS with Controlled Norm of the Hessian Approximation

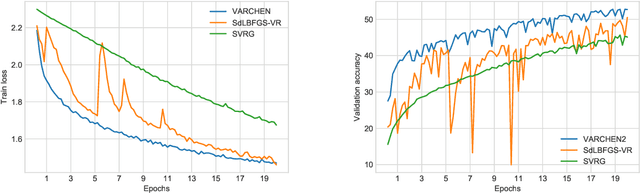
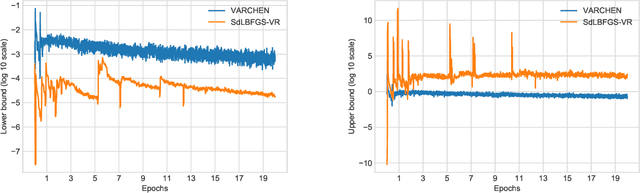
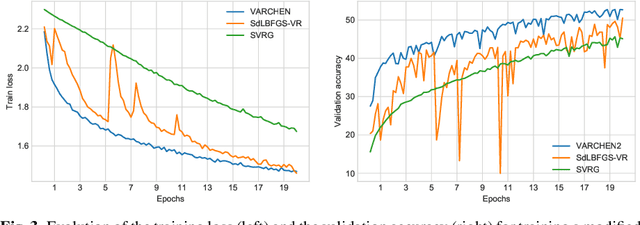
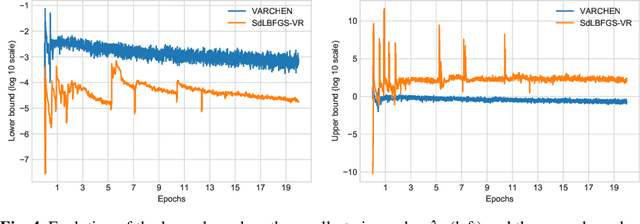
We propose a new stochastic variance-reduced damped L-BFGS algorithm, where we leverage estimates of bounds on the largest and smallest eigenvalues of the Hessian approximation to balance its quality and conditioning. Our algorithm, VARCHEN, draws from previous work that proposed a novel stochastic damped L-BFGS algorithm called SdLBFGS. We establish almost sure convergence to a stationary point and a complexity bound. We empirically demonstrate that VARCHEN is more robust than SdLBFGS-VR and SVRG on a modified DavidNet problem -- a highly nonconvex and ill-conditioned problem that arises in the context of deep learning, and their performance is comparable on a logistic regression problem and a nonconvex support-vector machine problem.