Adaptive First- and Second-Order Algorithms for Large-Scale Machine Learning
Paper and Code
Nov 29, 2021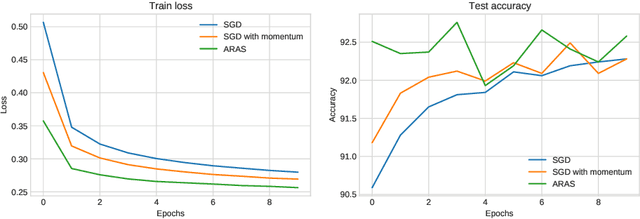
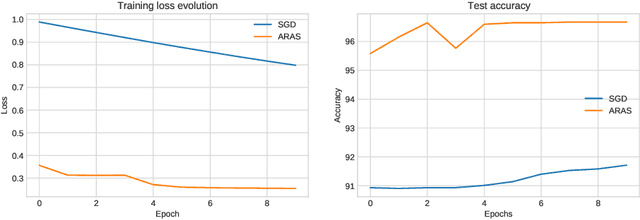
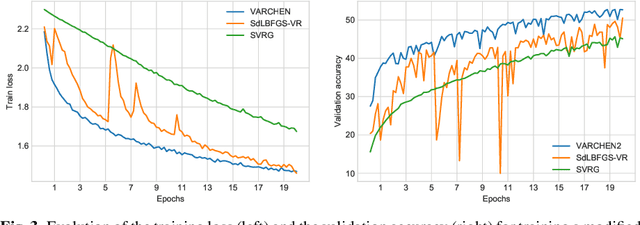
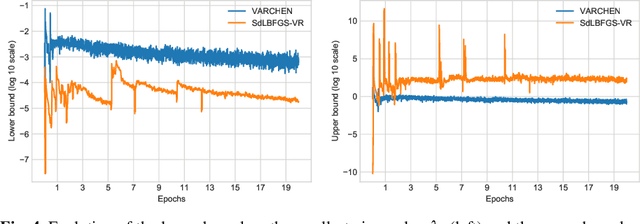
In this paper, we consider both first- and second-order techniques to address continuous optimization problems arising in machine learning. In the first-order case, we propose a framework of transition from deterministic or semi-deterministic to stochastic quadratic regularization methods. We leverage the two-phase nature of stochastic optimization to propose a novel first-order algorithm with adaptive sampling and adaptive step size. In the second-order case, we propose a novel stochastic damped L-BFGS method that improves on previous algorithms in the highly nonconvex context of deep learning. Both algorithms are evaluated on well-known deep learning datasets and exhibit promising performance.
* 29 pages, 8 figures. arXiv admin note: text overlap with
arXiv:2012.05783
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge