Asymptotic normality and optimalities in estimation of large Gaussian graphical models

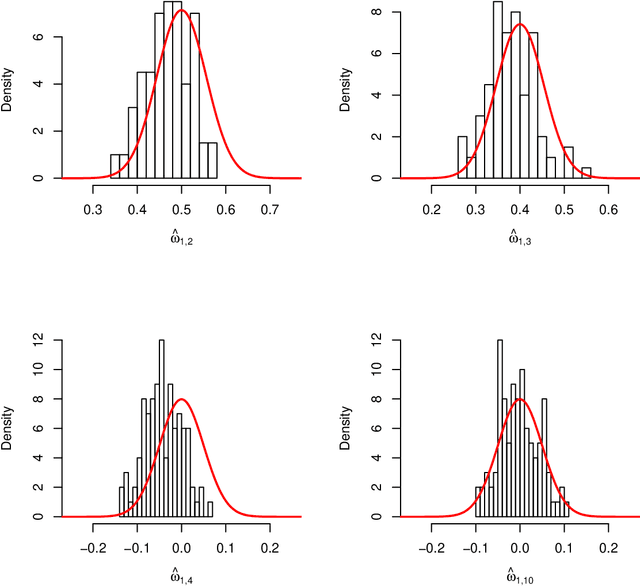
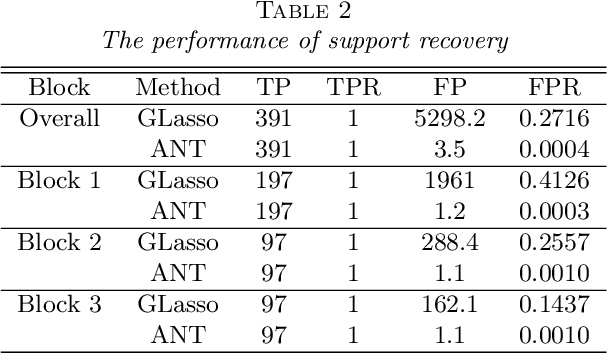
The Gaussian graphical model, a popular paradigm for studying relationship among variables in a wide range of applications, has attracted great attention in recent years. This paper considers a fundamental question: When is it possible to estimate low-dimensional parameters at parametric square-root rate in a large Gaussian graphical model? A novel regression approach is proposed to obtain asymptotically efficient estimation of each entry of a precision matrix under a sparseness condition relative to the sample size. When the precision matrix is not sufficiently sparse, or equivalently the sample size is not sufficiently large, a lower bound is established to show that it is no longer possible to achieve the parametric rate in the estimation of each entry. This lower bound result, which provides an answer to the delicate sample size question, is established with a novel construction of a subset of sparse precision matrices in an application of Le Cam's lemma. Moreover, the proposed estimator is proven to have optimal convergence rate when the parametric rate cannot be achieved, under a minimal sample requirement. The proposed estimator is applied to test the presence of an edge in the Gaussian graphical model or to recover the support of the entire model, to obtain adaptive rate-optimal estimation of the entire precision matrix as measured by the matrix $\ell_q$ operator norm and to make inference in latent variables in the graphical model. All of this is achieved under a sparsity condition on the precision matrix and a side condition on the range of its spectrum. This significantly relaxes the commonly imposed uniform signal strength condition on the precision matrix, irrepresentability condition on the Hessian tensor operator of the covariance matrix or the $\ell_1$ constraint on the precision matrix. Numerical results confirm our theoretical findings. The ROC curve of the proposed algorithm, Asymptotic Normal Thresholding (ANT), for support recovery significantly outperforms that of the popular GLasso algorithm.

Sparse Matrix Inversion with Scaled Lasso

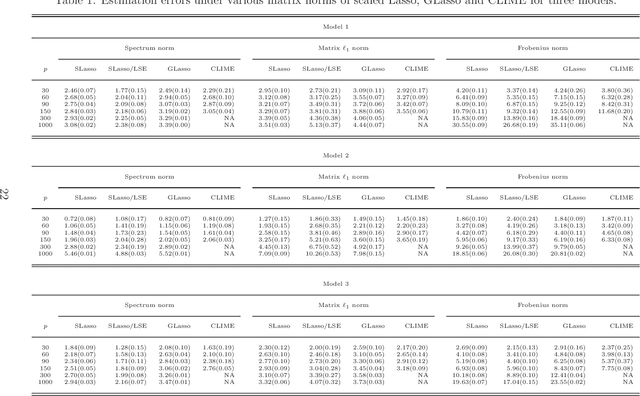
We propose a new method of learning a sparse nonnegative-definite target matrix. Our primary example of the target matrix is the inverse of a population covariance or correlation matrix. The algorithm first estimates each column of the target matrix by the scaled Lasso and then adjusts the matrix estimator to be symmetric. The penalty level of the scaled Lasso for each column is completely determined by data via convex minimization, without using cross-validation. We prove that this scaled Lasso method guarantees the fastest proven rate of convergence in the spectrum norm under conditions of weaker form than those in the existing analyses of other $\ell_1$ regularized algorithms, and has faster guaranteed rate of convergence when the ratio of the $\ell_1$ and spectrum norms of the target inverse matrix diverges to infinity. A simulation study demonstrates the computational feasibility and superb performance of the proposed method. Our analysis also provides new performance bounds for the Lasso and scaled Lasso to guarantee higher concentration of the error at a smaller threshold level than previous analyses, and to allow the use of the union bound in column-by-column applications of the scaled Lasso without an adjustment of the penalty level. In addition, the least squares estimation after the scaled Lasso selection is considered and proven to guarantee performance bounds similar to that of the scaled Lasso.

Calibrated Elastic Regularization in Matrix Completion

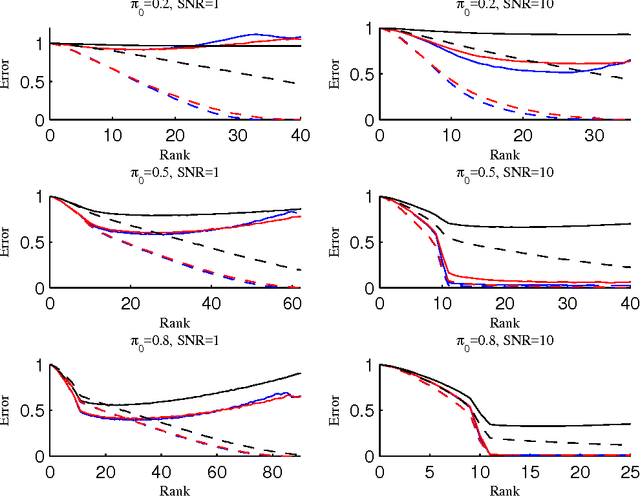
This paper concerns the problem of matrix completion, which is to estimate a matrix from observations in a small subset of indices. We propose a calibrated spectrum elastic net method with a sum of the nuclear and Frobenius penalties and develop an iterative algorithm to solve the convex minimization problem. The iterative algorithm alternates between imputing the missing entries in the incomplete matrix by the current guess and estimating the matrix by a scaled soft-thresholding singular value decomposition of the imputed matrix until the resulting matrix converges. A calibration step follows to correct the bias caused by the Frobenius penalty. Under proper coherence conditions and for suitable penalties levels, we prove that the proposed estimator achieves an error bound of nearly optimal order and in proportion to the noise level. This provides a unified analysis of the noisy and noiseless matrix completion problems. Simulation results are presented to compare our proposal with previous ones.

Scaled Sparse Linear Regression

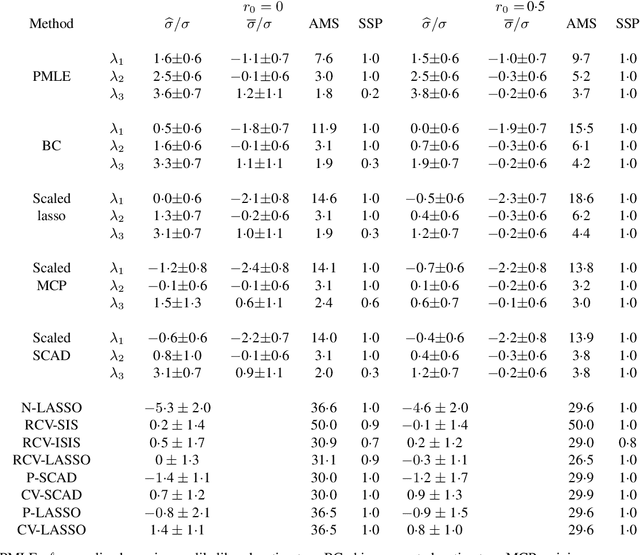
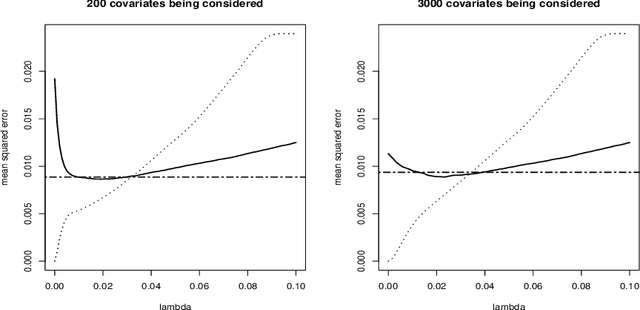
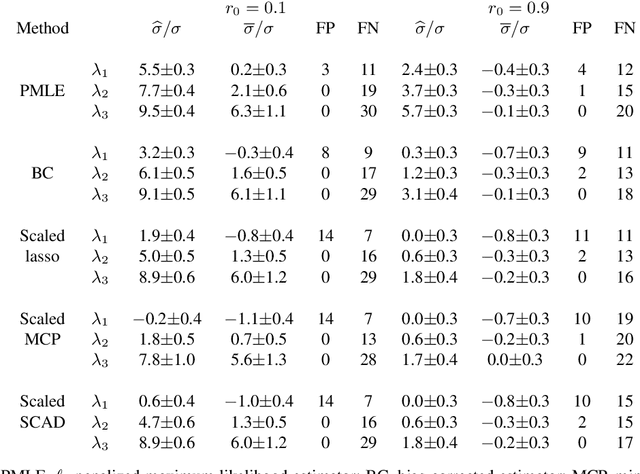
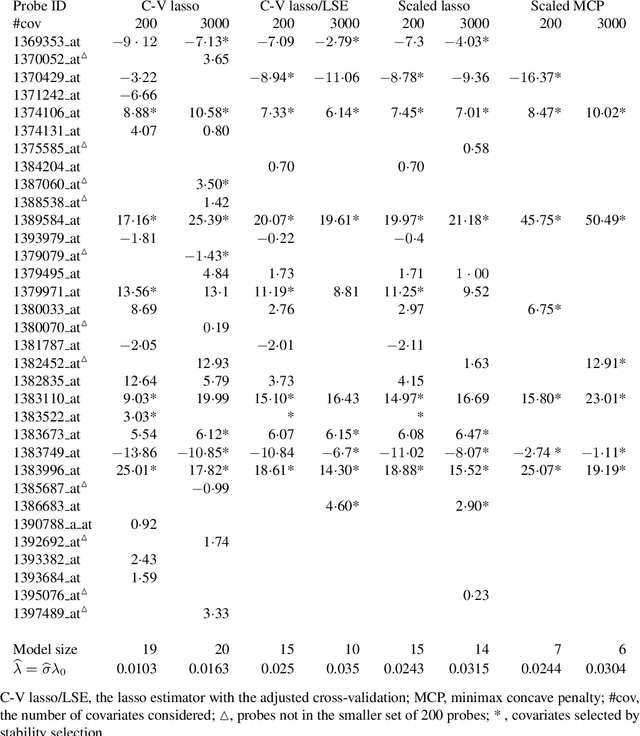
Scaled sparse linear regression jointly estimates the regression coefficients and noise level in a linear model. It chooses an equilibrium with a sparse regression method by iteratively estimating the noise level via the mean residual square and scaling the penalty in proportion to the estimated noise level. The iterative algorithm costs little beyond the computation of a path or grid of the sparse regression estimator for penalty levels above a proper threshold. For the scaled lasso, the algorithm is a gradient descent in a convex minimization of a penalized joint loss function for the regression coefficients and noise level. Under mild regularity conditions, we prove that the scaled lasso simultaneously yields an estimator for the noise level and an estimated coefficient vector satisfying certain oracle inequalities for prediction, the estimation of the noise level and the regression coefficients. These inequalities provide sufficient conditions for the consistency and asymptotic normality of the noise level estimator, including certain cases where the number of variables is of greater order than the sample size. Parallel results are provided for the least squares estimation after model selection by the scaled lasso. Numerical results demonstrate the superior performance of the proposed methods over an earlier proposal of joint convex minimization.