Few-Shot Action Localization without Knowing Boundaries

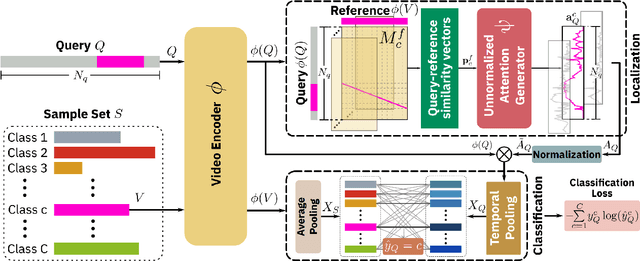
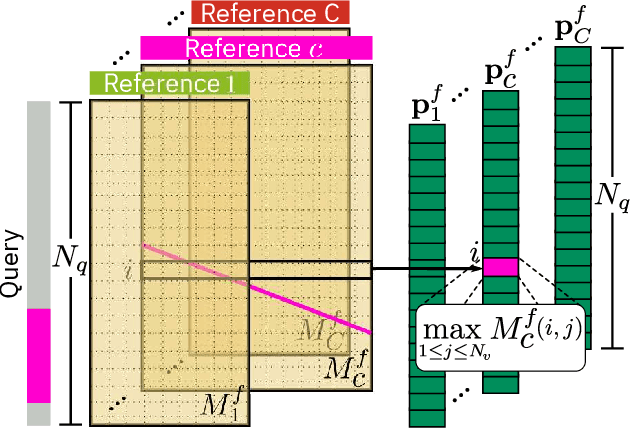
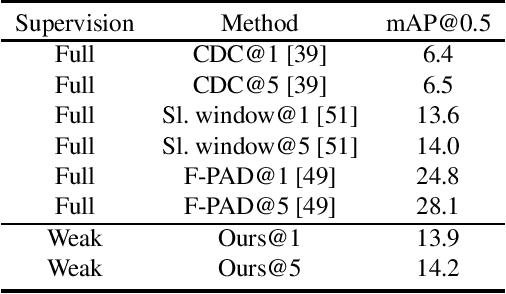
Learning to localize actions in long, cluttered, and untrimmed videos is a hard task, that in the literature has typically been addressed assuming the availability of large amounts of annotated training samples for each class -- either in a fully-supervised setting, where action boundaries are known, or in a weakly-supervised setting, where only class labels are known for each video. In this paper, we go a step further and show that it is possible to learn to localize actions in untrimmed videos when a) only one/few trimmed examples of the target action are available at test time, and b) when a large collection of videos with only class label annotation (some trimmed and some weakly annotated untrimmed ones) are available for training; with no overlap between the classes used during training and testing. To do so, we propose a network that learns to estimate Temporal Similarity Matrices (TSMs) that model a fine-grained similarity pattern between pairs of videos (trimmed or untrimmed), and uses them to generate Temporal Class Activation Maps (TCAMs) for seen or unseen classes. The TCAMs serve as temporal attention mechanisms to extract video-level representations of untrimmed videos, and to temporally localize actions at test time. To the best of our knowledge, we are the first to propose a weakly-supervised, one/few-shot action localization network that can be trained in an end-to-end fashion. Experimental results on THUMOS14 and ActivityNet1.2 datasets, show that our method achieves performance comparable or better to state-of-the-art fully-supervised, few-shot learning methods.

Temporal Action Localization with Variance-Aware Networks

This work addresses the problem of temporal action localization with Variance-Aware Networks (VAN), i.e., DNNs that use second-order statistics in the input and/or the output of regression tasks. We first propose a network (VANp) that when presented with the second-order statistics of the input, i.e., each sample has a mean and a variance, it propagates the mean and the variance throughout the network to deliver outputs with second order statistics. In this framework, both the input and the output could be interpreted as Gaussians. To do so, we derive differentiable analytic solutions, or reasonable approximations, to propagate across commonly used NN layers. To train the network, we define a differentiable loss based on the KL-divergence between the predicted Gaussian and a Gaussian around the ground truth action borders, and use standard back-propagation. Importantly, the variances propagation in VANp does not require any additional parameters, and during testing, does not require any additional computations either. In action localization, the means and the variances of the input are computed at pooling operations, that are typically used to bring arbitrarily long videos to a vector with fixed dimensions. Second, we propose two alternative formulations that augment the first (respectively, the last) layer of a regression network with additional parameters so as to take in the input (respectively, predict in the output) both means and variances. Results in the action localization problem show that the incorporation of second order statistics improves over the baseline network, and that VANp surpasses the accuracy of virtually all other two-stage networks without involving any additional parameters.

Boundary Uncertainty in a Single-Stage Temporal Action Localization Network

In this paper, we address the problem of temporal action localization with a single stage neural network. In the proposed architecture we model the boundary predictions as uni-variate Gaussian distributions in order to model their uncertainties, which is the first in this area to the best of our knowledge. We use two uncertainty-aware boundary regression losses: first, the Kullback-Leibler divergence between the ground truth location of the boundary and the Gaussian modeling the prediction of the boundary and second, the expectation of the $\ell_1$ loss under the same Gaussian. We show that with both uncertainty modeling approaches improve the detection performance by more than $1.5\%$ in mAP@tIoU=0.5 and that the proposed simple one-stage network performs closely to more complex one and two stage networks.