Causality and independence in perfectly adapted dynamical systems

Perfect adaptation in a dynamical system is the phenomenon that one or more variables have an initial transient response to a persistent change in an external stimulus but revert to their original value as the system converges to equilibrium. The causal ordering algorithm can be used to construct an equilibrium causal ordering graph that represents causal relations and a Markov ordering graph that implies conditional independences from a set of equilibrium equations. Based on this, we formulate sufficient graphical conditions to identify perfect adaptation from a set of first-order differential equations. Furthermore, we give sufficient conditions to test for the presence of perfect adaptation in experimental equilibrium data. We apply our ideas to a simple model for a protein signalling pathway and test its predictions both in simulations and on real-world protein expression data. We demonstrate that perfect adaptation in this model can explain why the presence and orientation of edges in the output of causal discovery algorithms does not always appear to agree with the direction of edges in biological consensus networks.

Robustness of Model Predictions under Extension

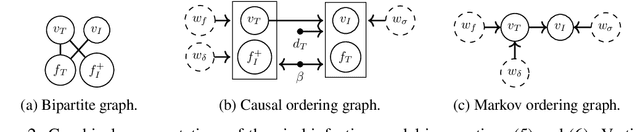
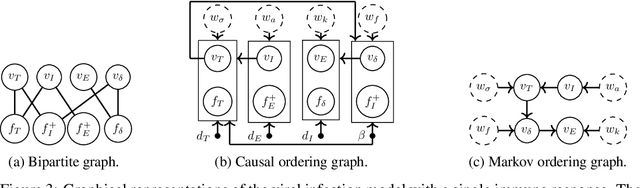
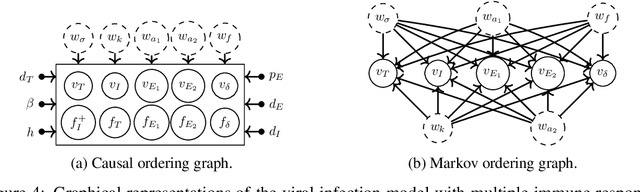
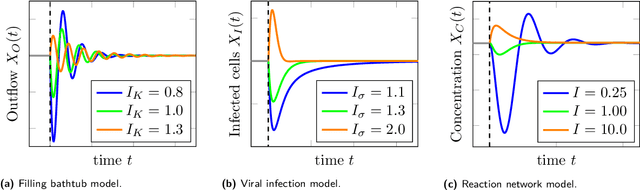
Often, mathematical models of the real world are simplified representations of complex systems. A caveat to using models for analysis is that predicted causal effects and conditional independences may not be robust under model extensions, and therefore applicability of such models is limited. In this work, we consider conditions under which qualitative model predictions are preserved when two models are combined. We show how to use the technique of causal ordering to efficiently assess the robustness of qualitative model predictions and characterize a large class of model extensions that preserve these predictions. For dynamical systems at equilibrium, we demonstrate how novel insights help to select appropriate model extensions and to reason about the presence of feedback loops. We apply our ideas to a viral infection model with immune responses.

Conditional Independences and Causal Relations implied by Sets of Equations

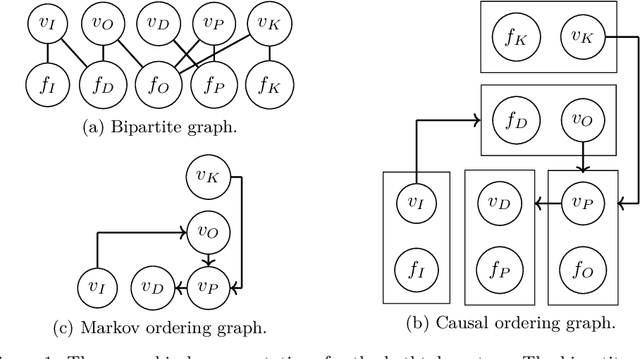
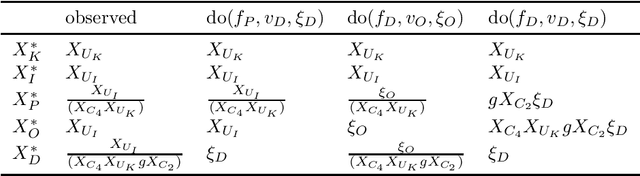
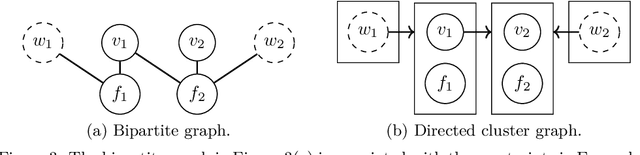
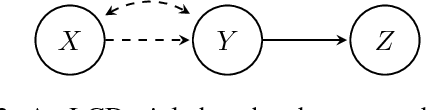
Real-world systems are often modelled by sets of equations with exogenous random variables. What can we say about the probabilistic and causal aspects of variables that appear in these equations without explicitly solving for them? We prove that, under a solvability assumption, we can construct a Markov ordering graph that implies conditional independences and a causal ordering graph that encodes the effects of soft and perfect interventions by making use of Simon's causal ordering algorithm. Our results shed new light on discussions in causal discovery about the justification of using graphs to simultaneously represent conditional independences and causal relations in models with feedback.

An Upper Bound for Random Measurement Error in Causal Discovery

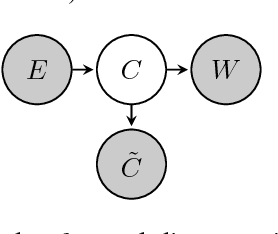
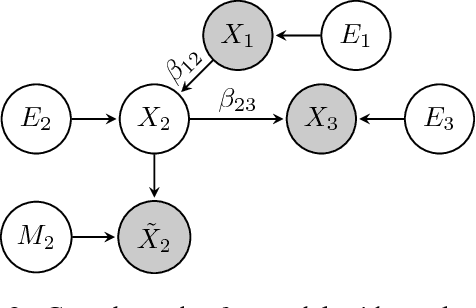
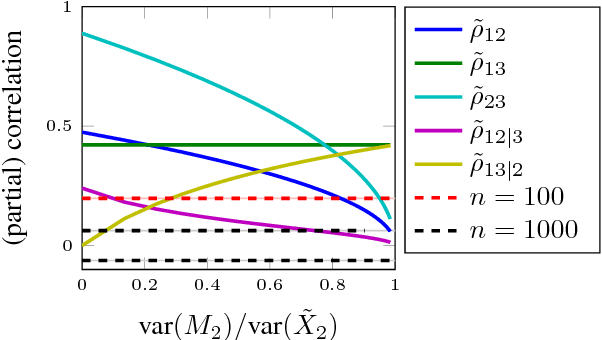
Causal discovery algorithms infer causal relations from data based on several assumptions, including notably the absence of measurement error. However, this assumption is most likely violated in practical applications, which may result in erroneous, irreproducible results. In this work we show how to obtain an upper bound for the variance of random measurement error from the covariance matrix of measured variables and how to use this upper bound as a correction for constraint-based causal discovery. We demonstrate a practical application of our approach on both simulated data and real-world protein signaling data.

Generalized Strucutral Causal Models

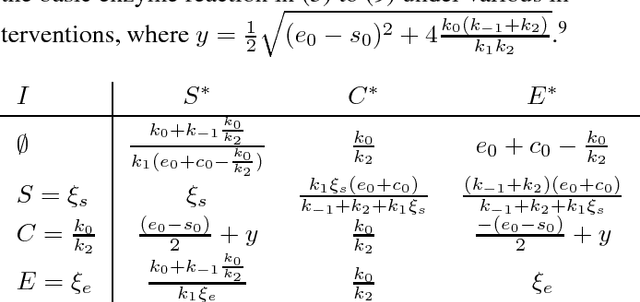
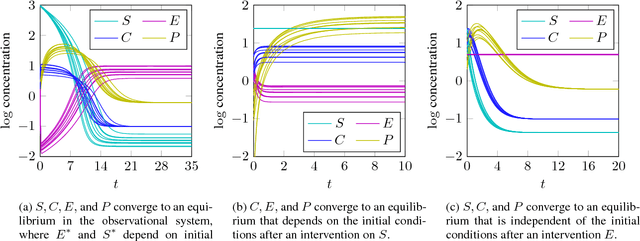
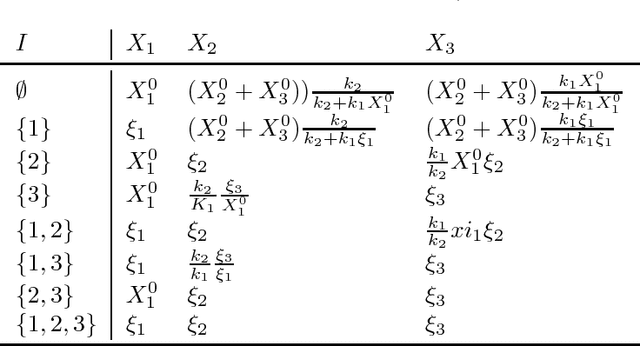
Structural causal models are a popular tool to describe causal relations in systems in many fields such as economy, the social sciences, and biology. In this work, we show that these models are not flexible enough in general to give a complete causal representation of equilibrium states in dynamical systems that do not have a unique stable equilibrium independent of initial conditions. We prove that our proposed generalized structural causal models do capture the essential causal semantics that characterize these systems. We illustrate the power and flexibility of this extension on a dynamical system corresponding to a basic enzymatic reaction. We motivate our approach further by showing that it also efficiently describes the effects of interventions on functional laws such as the ideal gas law.