Conditional Independences and Causal Relations implied by Sets of Equations

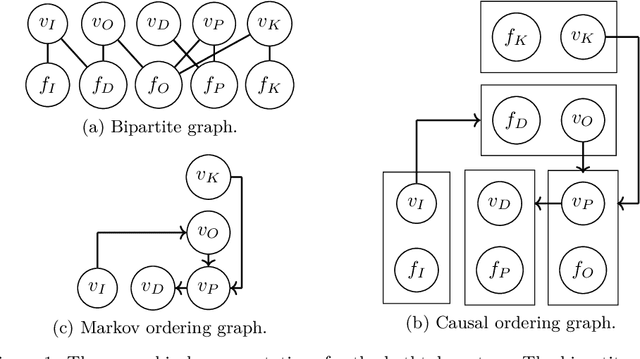
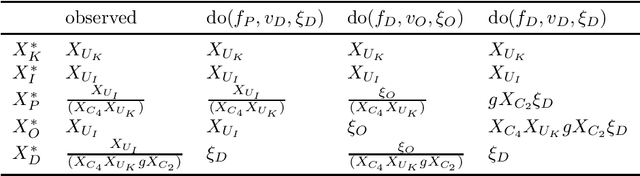
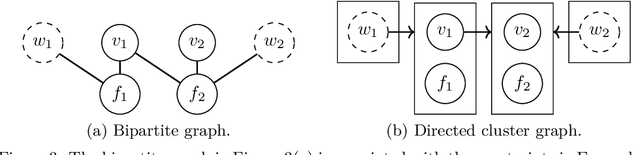
Real-world systems are often modelled by sets of equations with exogenous random variables. What can we say about the probabilistic and causal aspects of variables that appear in these equations without explicitly solving for them? We prove that, under a solvability assumption, we can construct a Markov ordering graph that implies conditional independences and a causal ordering graph that encodes the effects of soft and perfect interventions by making use of Simon's causal ordering algorithm. Our results shed new light on discussions in causal discovery about the justification of using graphs to simultaneously represent conditional independences and causal relations in models with feedback.