Robustness of Model Predictions under Extension

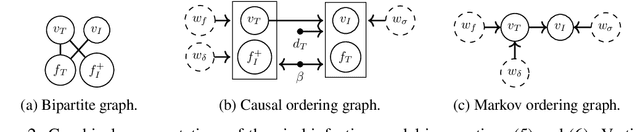
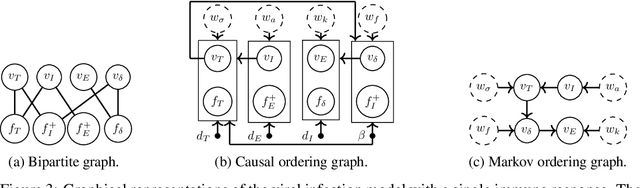
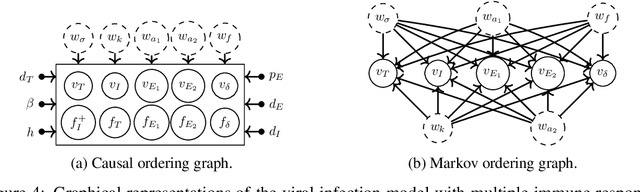
Often, mathematical models of the real world are simplified representations of complex systems. A caveat to using models for analysis is that predicted causal effects and conditional independences may not be robust under model extensions, and therefore applicability of such models is limited. In this work, we consider conditions under which qualitative model predictions are preserved when two models are combined. We show how to use the technique of causal ordering to efficiently assess the robustness of qualitative model predictions and characterize a large class of model extensions that preserve these predictions. For dynamical systems at equilibrium, we demonstrate how novel insights help to select appropriate model extensions and to reason about the presence of feedback loops. We apply our ideas to a viral infection model with immune responses.