Timothy A. Smith
Temporal Subsampling Diminishes Small Spatial Scales in Recurrent Neural Network Emulators of Geophysical Turbulence
Apr 28, 2023Abstract:The immense computational cost of traditional numerical weather and climate models has sparked the development of machine learning (ML) based emulators. Because ML methods benefit from long records of training data, it is common to use datasets that are temporally subsampled relative to the time steps required for the numerical integration of differential equations. Here, we investigate how this often overlooked processing step affects the quality of an emulator's predictions. We implement two ML architectures from a class of methods called reservoir computing: (1) a form of Nonlinear Vector Autoregression (NVAR), and (2) an Echo State Network (ESN). Despite their simplicity, it is well documented that these architectures excel at predicting low dimensional chaotic dynamics. We are therefore motivated to test these architectures in an idealized setting of predicting high dimensional geophysical turbulence as represented by Surface Quasi-Geostrophic dynamics. In all cases, subsampling the training data consistently leads to an increased bias at small spatial scales that resembles numerical diffusion. Interestingly, the NVAR architecture becomes unstable when the temporal resolution is increased, indicating that the polynomial based interactions are insufficient at capturing the detailed nonlinearities of the turbulent flow. The ESN architecture is found to be more robust, suggesting a benefit to the more expensive but more general structure. Spectral errors are reduced by including a penalty on the kinetic energy density spectrum during training, although the subsampling related errors persist. Future work is warranted to understand how the temporal resolution of training data affects other ML architectures.
Constraining Chaos: Enforcing dynamical invariants in the training of recurrent neural networks
Apr 24, 2023Abstract:Drawing on ergodic theory, we introduce a novel training method for machine learning based forecasting methods for chaotic dynamical systems. The training enforces dynamical invariants--such as the Lyapunov exponent spectrum and fractal dimension--in the systems of interest, enabling longer and more stable forecasts when operating with limited data. The technique is demonstrated in detail using the recurrent neural network architecture of reservoir computing. Results are given for the Lorenz 1996 chaotic dynamical system and a spectral quasi-geostrophic model, both typical test cases for numerical weather prediction.
A Systematic Exploration of Reservoir Computing for Forecasting Complex Spatiotemporal Dynamics
Jan 21, 2022


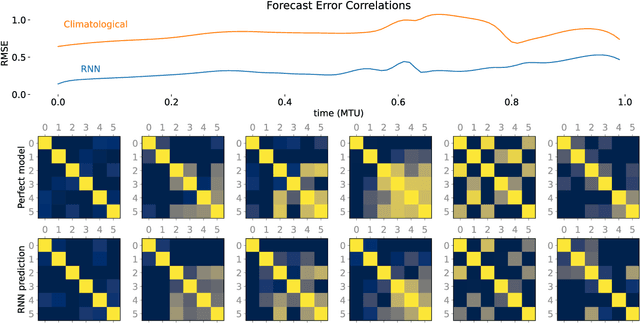
Abstract:A reservoir computer (RC) is a type of simplified recurrent neural network architecture that has demonstrated success in the prediction of spatiotemporally chaotic dynamical systems. A further advantage of RC is that it reproduces intrinsic dynamical quantities essential for its incorporation into numerical forecasting routines such as the ensemble Kalman filter -- used in numerical weather prediction to compensate for sparse and noisy data. We explore here the architecture and design choices for a "best in class" RC for a number of characteristic dynamical systems, and then show the application of these choices in scaling up to larger models using localization. Our analysis points to the importance of large scale parameter optimization. We also note in particular the importance of including input bias in the RC design, which has a significant impact on the forecast skill of the trained RC model. In our tests, the the use of a nonlinear readout operator does not affect the forecast time or the stability of the forecast. The effects of the reservoir dimension, spinup time, amount of training data, normalization, noise, and the RC time step are also investigated. While we are not aware of a generally accepted best reported mean forecast time for different models in the literature, we report over a factor of 2 increase in the mean forecast time compared to the best performing RC model of Vlachas et.al (2020) for the 40 dimensional spatiotemporally chaotic Lorenz 1996 dynamics, and we are able to accomplish this using a smaller reservoir size.
`Next Generation' Reservoir Computing: an Empirical Data-Driven Expression of Dynamical Equations in Time-Stepping Form
Jan 13, 2022



Abstract:Next generation reservoir computing based on nonlinear vector autoregression (NVAR) is applied to emulate simple dynamical system models and compared to numerical integration schemes such as Euler and the $2^\text{nd}$ order Runge-Kutta. It is shown that the NVAR emulator can be interpreted as a data-driven method used to recover the numerical integration scheme that produced the data. It is also shown that the approach can be extended to produce high-order numerical schemes directly from data. The impacts of the presence of noise and temporal sparsity in the training set is further examined to gauge the potential use of this method for more realistic applications.
Integrating Recurrent Neural Networks with Data Assimilation for Scalable Data-Driven State Estimation
Sep 25, 2021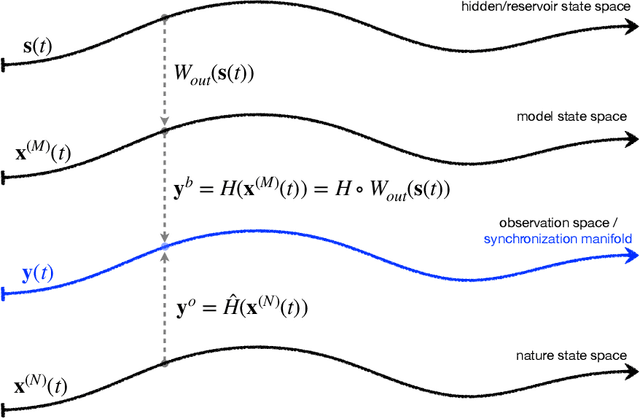

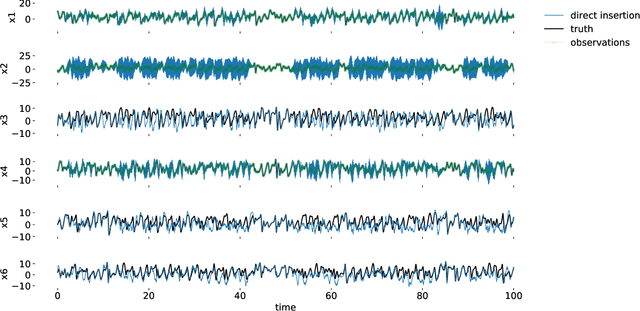
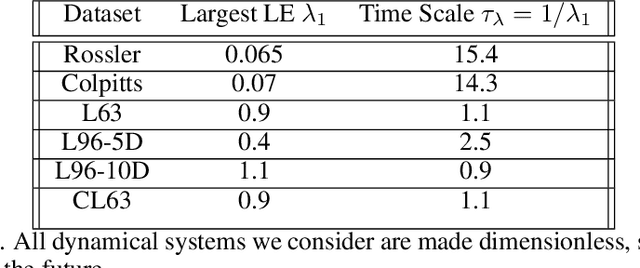
Abstract:Data assimilation (DA) is integrated with machine learning in order to perform entirely data-driven online state estimation. To achieve this, recurrent neural networks (RNNs) are implemented as surrogate models to replace key components of the DA cycle in numerical weather prediction (NWP), including the conventional numerical forecast model, the forecast error covariance matrix, and the tangent linear and adjoint models. It is shown how these RNNs can be initialized using DA methods to directly update the hidden/reservoir state with observations of the target system. The results indicate that these techniques can be applied to estimate the state of a system for the repeated initialization of short-term forecasts, even in the absence of a traditional numerical forecast model. Further, it is demonstrated how these integrated RNN-DA methods can scale to higher dimensions by applying domain localization and parallelization, providing a path for practical applications in NWP.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge