A Systematic Exploration of Reservoir Computing for Forecasting Complex Spatiotemporal Dynamics

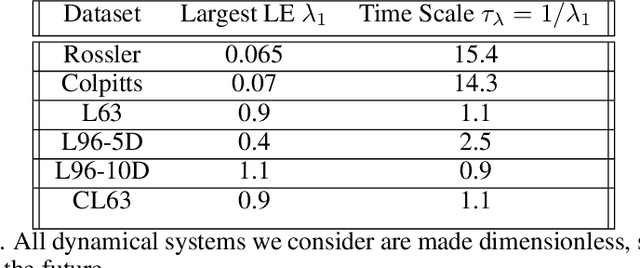
A reservoir computer (RC) is a type of simplified recurrent neural network architecture that has demonstrated success in the prediction of spatiotemporally chaotic dynamical systems. A further advantage of RC is that it reproduces intrinsic dynamical quantities essential for its incorporation into numerical forecasting routines such as the ensemble Kalman filter -- used in numerical weather prediction to compensate for sparse and noisy data. We explore here the architecture and design choices for a "best in class" RC for a number of characteristic dynamical systems, and then show the application of these choices in scaling up to larger models using localization. Our analysis points to the importance of large scale parameter optimization. We also note in particular the importance of including input bias in the RC design, which has a significant impact on the forecast skill of the trained RC model. In our tests, the the use of a nonlinear readout operator does not affect the forecast time or the stability of the forecast. The effects of the reservoir dimension, spinup time, amount of training data, normalization, noise, and the RC time step are also investigated. While we are not aware of a generally accepted best reported mean forecast time for different models in the literature, we report over a factor of 2 increase in the mean forecast time compared to the best performing RC model of Vlachas et.al (2020) for the 40 dimensional spatiotemporally chaotic Lorenz 1996 dynamics, and we are able to accomplish this using a smaller reservoir size.