Efficiently Training Neural Networks for Imperfect Information Games by Sampling Information Sets

In imperfect information games, the evaluation of a game state not only depends on the observable world but also relies on hidden parts of the environment. As accessing the obstructed information trivialises state evaluations, one approach to tackle such problems is to estimate the value of the imperfect state as a combination of all states in the information set, i.e., all possible states that are consistent with the current imperfect information. In this work, the goal is to learn a function that maps from the imperfect game information state to its expected value. However, constructing a perfect training set, i.e. an enumeration of the whole information set for numerous imperfect states, is often infeasible. To compute the expected values for an imperfect information game like \textit{Reconnaissance Blind Chess}, one would need to evaluate thousands of chess positions just to obtain the training target for a single state. Still, the expected value of a state can already be approximated with appropriate accuracy from a much smaller set of evaluations. Thus, in this paper, we empirically investigate how a budget of perfect information game evaluations should be distributed among training samples to maximise the return. Our results show that sampling a small number of states, in our experiments roughly 3, for a larger number of separate positions is preferable over repeatedly sampling a smaller quantity of states. Thus, we find that in our case, the quantity of different samples seems to be more important than higher target quality.

Neural Network-based Information Set Weighting for Playing Reconnaissance Blind Chess

In imperfect information games, the game state is generally not fully observable to players. Therefore, good gameplay requires policies that deal with the different information that is hidden from each player. To combat this, effective algorithms often reason about information sets; the sets of all possible game states that are consistent with a player's observations. While there is no way to distinguish between the states within an information set, this property does not imply that all states are equally likely to occur in play. We extend previous research on assigning weights to the states in an information set in order to facilitate better gameplay in the imperfect information game of Reconnaissance Blind Chess. For this, we train two different neural networks which estimate the likelihood of each state in an information set from historical game data. Experimentally, we find that a Siamese neural network is able to achieve higher accuracy and is more efficient than a classical convolutional neural network for the given domain. Finally, we evaluate an RBC-playing agent that is based on the generated weightings and compare different parameter settings that influence how strongly it should rely on them. The resulting best player is ranked 5th on the public leaderboard.

Contrastive Learning of Preferences with a Contextual InfoNCE Loss

A common problem in contextual preference ranking is that a single preferred action is compared against several choices, thereby blowing up the complexity and skewing the preference distribution. In this work, we show how one can solve this problem via a suitable adaptation of the CLIP framework.This adaptation is not entirely straight-forward, because although the InfoNCE loss used by CLIP has achieved great success in computer vision and multi-modal domains, its batch-construction technique requires the ability to compare arbitrary items, and is not well-defined if one item has multiple positive associations in the same batch. We empirically demonstrate the utility of our adapted version of the InfoNCE loss in the domain of collectable card games, where we aim to learn an embedding space that captures the associations between single cards and whole card pools based on human selections. Such selection data only exists for restricted choices, thus generating concrete preferences of one item over a set of other items rather than a perfect fit between the card and the pool. Our results show that vanilla CLIP does not perform well due to the aforementioned intuitive issues. However, by adapting CLIP to the problem, we receive a model outperforming previous work trained with the triplet loss, while also alleviating problems associated with mining triplets.

Learning With Generalised Card Representations for "Magic: The Gathering"

A defining feature of collectable card games is the deck building process prior to actual gameplay, in which players form their decks according to some restrictions. Learning to build decks is difficult for players and models alike due to the large card variety and highly complex semantics, as well as requiring meaningful card and deck representations when aiming to utilise AI. In addition, regular releases of new card sets lead to unforeseeable fluctuations in the available card pool, thus affecting possible deck configurations and requiring continuous updates. Previous Game AI approaches to building decks have often been limited to fixed sets of possible cards, which greatly limits their utility in practice. In this work, we explore possible card representations that generalise to unseen cards, thus greatly extending the real-world utility of AI-based deck building for the game "Magic: The Gathering".We study such representations based on numerical, nominal, and text-based features of cards, card images, and meta information about card usage from third-party services. Our results show that while the particular choice of generalised input representation has little effect on learning to predict human card selections among known cards, the performance on new, unseen cards can be greatly improved. Our generalised model is able to predict 55\% of human choices on completely unseen cards, thus showing a deep understanding of card quality and strategy.

Supervised and Reinforcement Learning from Observations in Reconnaissance Blind Chess

In this work, we adapt a training approach inspired by the original AlphaGo system to play the imperfect information game of Reconnaissance Blind Chess. Using only the observations instead of a full description of the game state, we first train a supervised agent on publicly available game records. Next, we increase the performance of the agent through self-play with the on-policy reinforcement learning algorithm Proximal Policy Optimization. We do not use any search to avoid problems caused by the partial observability of game states and only use the policy network to generate moves when playing. With this approach, we achieve an ELO of 1330 on the RBC leaderboard, which places our agent at position 27 at the time of this writing. We see that self-play significantly improves performance and that the agent plays acceptably well without search and without making assumptions about the true game state.

Quantity vs Quality: Investigating the Trade-Off between Sample Size and Label Reliability

In this paper, we study learning in probabilistic domains where the learner may receive incorrect labels but can improve the reliability of labels by repeatedly sampling them. In such a setting, one faces the problem of whether the fixed budget for obtaining training examples should rather be used for obtaining all different examples or for improving the label quality of a smaller number of examples by re-sampling their labels. We motivate this problem in an application to compare the strength of poker hands where the training signal depends on the hidden community cards, and then study it in depth in an artificial setting where we insert controlled noise levels into the MNIST database. Our results show that with increasing levels of noise, resampling previous examples becomes increasingly more important than obtaining new examples, as classifier performance deteriorates when the number of incorrect labels is too high. In addition, we propose two different validation strategies; switching from lower to higher validations over the course of training and using chi-square statistics to approximate the confidence in obtained labels.

A Comparison of Contextual and Non-Contextual Preference Ranking for Set Addition Problems

In this paper, we study the problem of evaluating the addition of elements to a set. This problem is difficult, because it can, in the general case, not be reduced to unconditional preferences between the choices. Therefore, we model preferences based on the context of the decision. We discuss and compare two different Siamese network architectures for this task: a twin network that compares the two sets resulting after the addition, and a triplet network that models the contribution of each candidate to the existing set. We evaluate the two settings on a real-world task; learning human card preferences for deck building in the collectible card game Magic: The Gathering. We show that the triplet approach achieves a better result than the twin network and that both outperform previous results on this task.

Predicting Human Card Selection in Magic: The Gathering with Contextual Preference Ranking

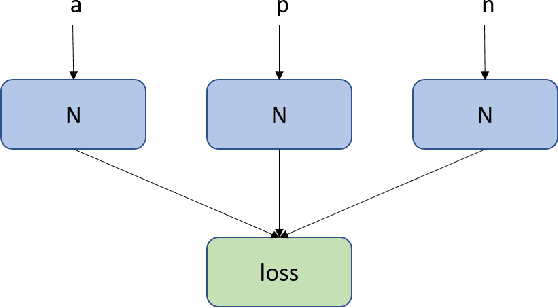
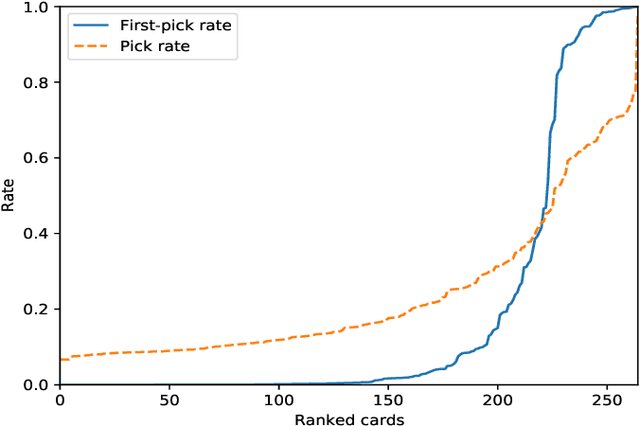
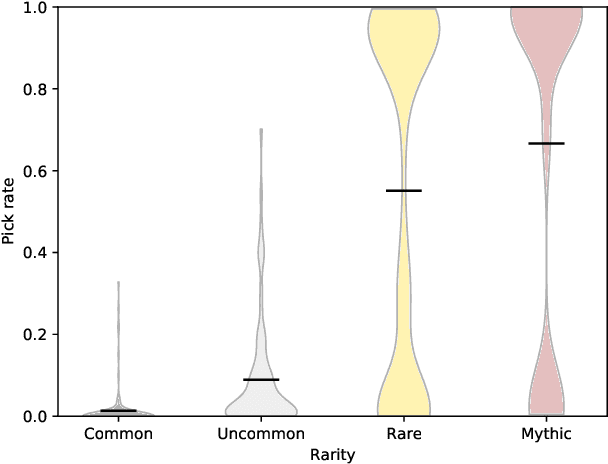
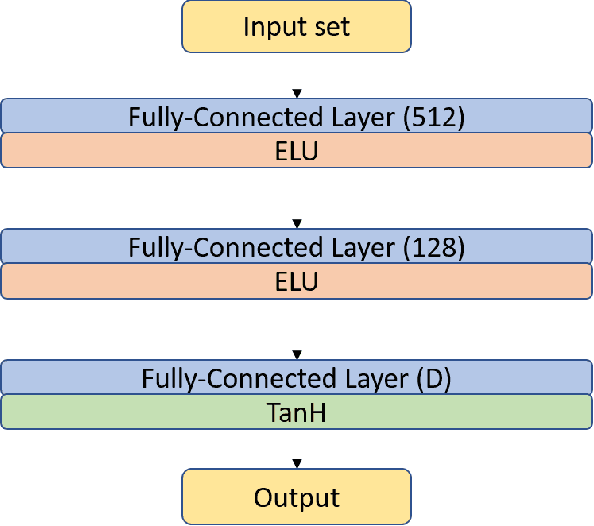
Drafting, i.e., the selection of a subset of items from a larger candidate set, is a key element of many games and related problems. It encompasses team formation in sports or e-sports, as well as deck selection in many modern card games. The key difficulty of drafting is that it is typically not sufficient to simply evaluate each item in a vacuum and to select the best items. The evaluation of an item depends on the context of the set of items that were already selected earlier, as the value of a set is not just the sum of the values of its members - it must include a notion of how well items go together. In this paper, we study drafting in the context of the card game Magic: The Gathering. We propose the use of a contextual preference network, which learns to compare two possible extensions of a given deck of cards. We demonstrate that the resulting network is better able to evaluate card decks in this game than previous attempts.