Weakly monotone averaging functions

Monotonicity with respect to all arguments is fundamental to the definition of aggregation functions. It is also a limiting property that results in many important non-monotonic averaging functions being excluded from the theoretical framework. This work proposes a definition for weakly monotonic averaging functions, studies some properties of this class of functions and proves that several families of important non-monotonic means are actually weakly monotonic averaging functions. Specifically we provide sufficient conditions for weak monotonicity of the Lehmer mean and generalised mixture operators. We establish weak monotonicity of several robust estimators of location and conditions for weak monotonicity of a large class of penalty-based aggregation functions. These results permit a proof of the weak monotonicity of the class of spatial-tonal filters that include important members such as the bilateral filter and anisotropic diffusion. Our concept of weak monotonicity provides a sound theoretical and practical basis by which (monotone) aggregation functions and non-monotone averaging functions can be related within the same framework, allowing us to bridge the gap between these previously disparate areas of research.

A Case Study in Knowledge Discovery and Elicitation in an Intelligent Tutoring Application

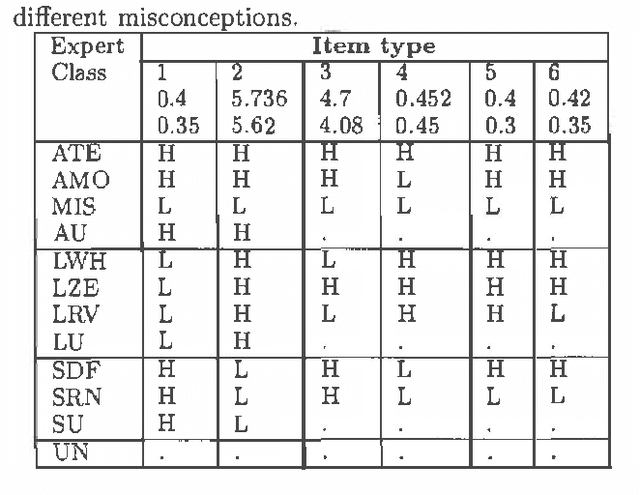
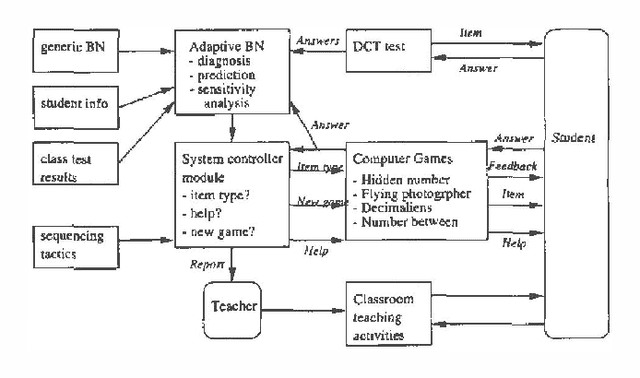
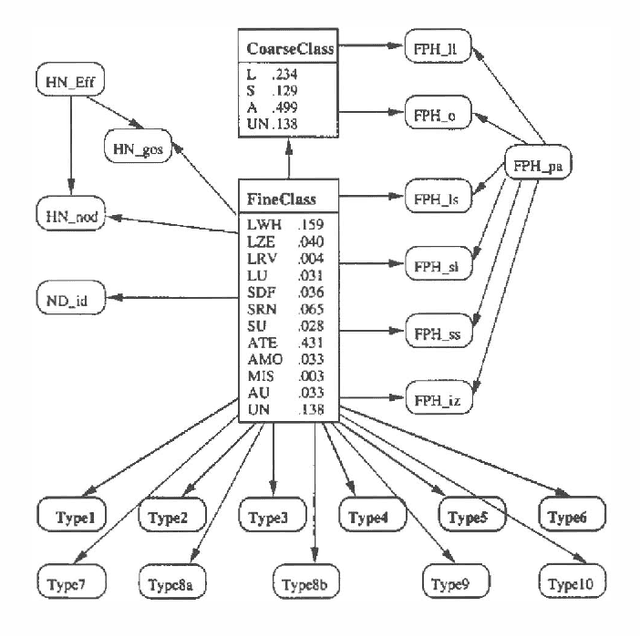
Most successful Bayesian network (BN) applications to datehave been built through knowledge elicitation from experts.This is difficult and time consuming, which has lead to recentinterest in automated methods for learning BNs from data. We present a case study in the construction of a BN in anintelligent tutoring application, specifically decimal misconceptions. Wedescribe the BN construction using expert elicitation and then investigate how certainexisting automated knowledge discovery methods might support the BN knowledge engineering process.