Measuring, Interpreting, and Improving Fairness of Algorithms using Causal Inference and Randomized Experiments

Algorithm fairness has become a central problem for the broad adoption of artificial intelligence. Although the past decade has witnessed an explosion of excellent work studying algorithm biases, achieving fairness in real-world AI production systems has remained a challenging task. Most existing works fail to excel in practical applications since either they have conflicting measurement techniques and/ or heavy assumptions, or require code-access of the production models, whereas real systems demand an easy-to-implement measurement framework and a systematic way to correct the detected sources of bias. In this paper, we leverage recent advances in causal inference and interpretable machine learning to present an algorithm-agnostic framework (MIIF) to Measure, Interpret, and Improve the Fairness of an algorithmic decision. We measure the algorithm bias using randomized experiments, which enables the simultaneous measurement of disparate treatment, disparate impact, and economic value. Furthermore, using modern interpretability techniques, we develop an explainable machine learning model which accurately interprets and distills the beliefs of a blackbox algorithm. Altogether, these techniques create a simple and powerful toolset for studying algorithm fairness, especially for understanding the cost of fairness in practical applications like e-commerce and targeted advertising, where industry A/B testing is already abundant.

Dimension-Free Average Treatment Effect Inference with Deep Neural Networks

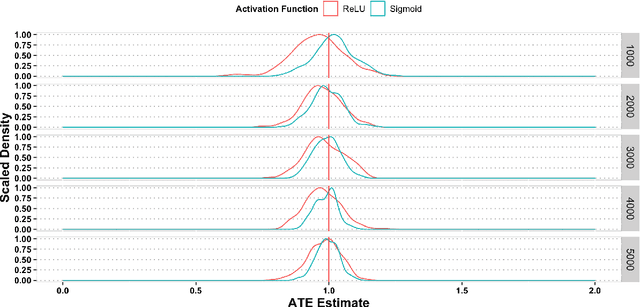
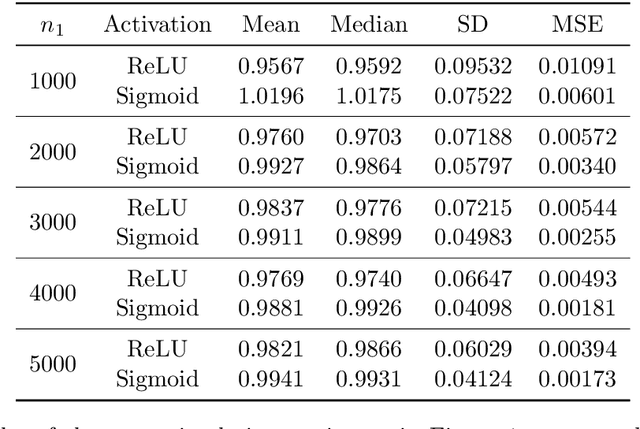
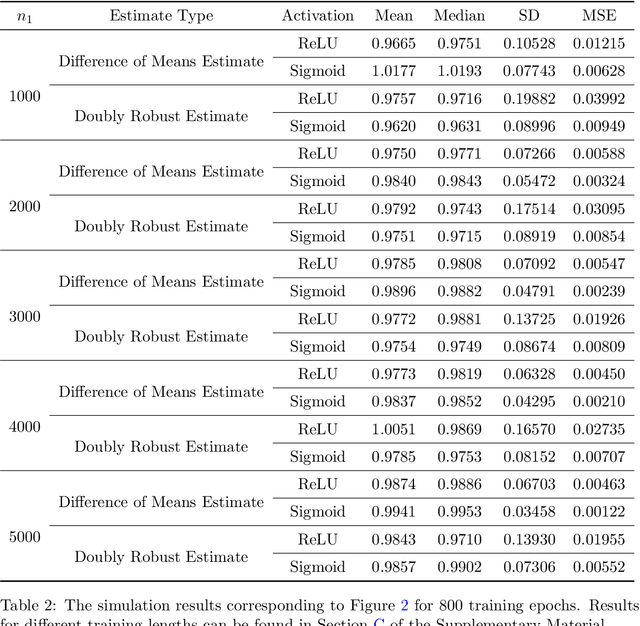
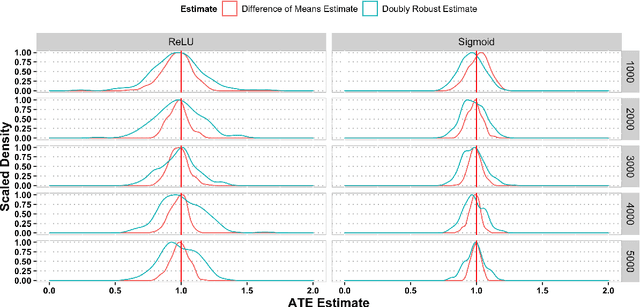
This paper investigates the estimation and inference of the average treatment effect (ATE) using deep neural networks (DNNs) in the potential outcomes framework. Under some regularity conditions, the observed response can be formulated as the response of a mean regression problem with both the confounding variables and the treatment indicator as the independent variables. Using such formulation, we investigate two methods for ATE estimation and inference based on the estimated mean regression function via DNN regression using a specific network architecture. We show that both DNN estimates of ATE are consistent with dimension-free consistency rates under some assumptions on the underlying true mean regression model. Our model assumptions accommodate the potentially complicated dependence structure of the observed response on the covariates, including latent factors and nonlinear interactions between the treatment indicator and confounding variables. We also establish the asymptotic normality of our estimators based on the idea of sample splitting, ensuring precise inference and uncertainty quantification. Simulation studies and real data application justify our theoretical findings and support our DNN estimation and inference methods.