Thomas Bailie
Reducing Smoothness with Expressive Memory Enhanced Hierarchical Graph Neural Networks
Apr 02, 2025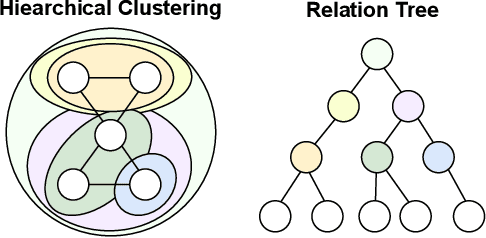
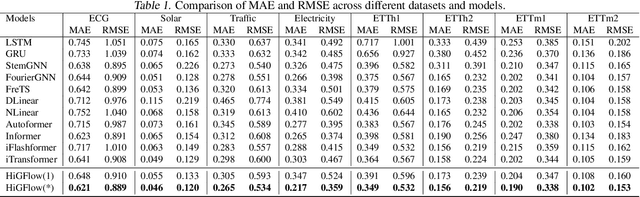
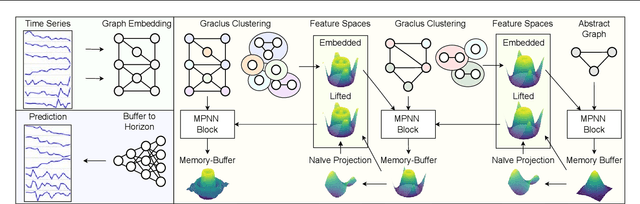
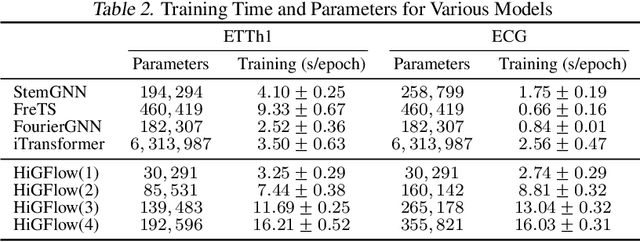
Abstract:Graphical forecasting models learn the structure of time series data via projecting onto a graph, with recent techniques capturing spatial-temporal associations between variables via edge weights. Hierarchical variants offer a distinct advantage by analysing the time series across multiple resolutions, making them particularly effective in tasks like global weather forecasting, where low-resolution variable interactions are significant. A critical challenge in hierarchical models is information loss during forward or backward passes through the hierarchy. We propose the Hierarchical Graph Flow (HiGFlow) network, which introduces a memory buffer variable of dynamic size to store previously seen information across variable resolutions. We theoretically show two key results: HiGFlow reduces smoothness when mapping onto new feature spaces in the hierarchy and non-strictly enhances the utility of message-passing by improving Weisfeiler-Lehman (WL) expressivity. Empirical results demonstrate that HiGFlow outperforms state-of-the-art baselines, including transformer models, by at least an average of 6.1% in MAE and 6.2% in RMSE. Code is available at https://github.com/TB862/ HiGFlow.git.
Higher Order Graph Attention Probabilistic Walk Networks
Nov 18, 2024Abstract:Graphs inherently capture dependencies between nodes or variables through their topological structure, with paths between any two nodes indicating a sequential dependency on the nodes traversed. Message Passing Neural Networks (MPNNs) leverage these latent relationships embedded in graph structures, and have become widely adopted across diverse applications. However, many existing methods predominantly rely on local information within the $1$-hop neighborhood. This approach has notable limitations; for example, $1$-hop aggregation schemes inherently lose long-distance information, and are limited in expressive power as defined by the $k$-Weisfeiler-Leman ($k$-WL) isomorphism test. To address these issues, we propose the Higher Order Graphical Attention (HoGA) module, which assigns weights to variable-length paths sampled based on feature-vector diversity, effectively reconstructing the $k$-hop neighborhood. HoGA represents higher-order relationships as a robust form of self-attention, applicable to any single-hop attention mechanism. In empirical studies, applying HoGA to existing attention-based models consistently leads to significant accuracy improvements on benchmark node classification datasets. Furthermore, we observe that the performance degradation typically associated with additional message-passing steps may be mitigated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge