Unsatisfiable Cores and Lower Bounding for Constraint Programming

Constraint Programming (CP) solvers typically tackle optimization problems by repeatedly finding solutions to a problem while placing tighter and tighter bounds on the solution cost. This approach is somewhat naive, especially for soft-constraint optimization problems in which the soft constraints are mostly satisfied. Unsatisfiable-core approaches to solving soft constraint problems in SAT (e.g. MAXSAT) force all soft constraints to be hard initially. When solving fails they return an unsatisfiable core, as a set of soft constraints that cannot hold simultaneously. These are reverted to soft and solving continues. Since lazy clause generation solvers can also return unsatisfiable cores we can adapt this approach to constraint programming. We adapt the original MAXSAT unsatisfiable core solving approach to be usable for constraint programming and define a number of extensions. Experimental results show that our methods are beneficial on a broad class of CP-optimization benchmarks involving soft constraints, cardinality or preferences.

Unsatisfiable Cores for Constraint Programming

Constraint Programming (CP) solvers typically tackle optimization problems by repeatedly finding solutions to a problem while placing tighter and tighter bounds on the solution cost. This approach is somewhat naive, especially for soft-constraint optimization problems in which the soft constraints are mostly satisfied. Unsatisfiable-core approaches to solving soft constraint problems in Boolean Satisfiability (e.g. MAXSAT) force all soft constraints to hold initially. When solving fails they return an unsatisfiable core, as a set of soft constraints that cannot hold simultaneously. Using this information the problem is relaxed to allow certain soft constraint(s) to be violated and solving continues. Since Lazy Clause Generation (LCG) solvers can also return unsatisfiable cores we can adapt the MAXSAT unsatisfiable core approach to CP. We implement the original MAXSAT unsatisfiable core solving algorithms WPM1, MSU3 in a state-of-the-art LCG solver and show that there exist problems which benefit from this hybrid approach.

Explaining Time-Table-Edge-Finding Propagation for the Cumulative Resource Constraint

Cumulative resource constraints can model scarce resources in scheduling problems or a dimension in packing and cutting problems. In order to efficiently solve such problems with a constraint programming solver, it is important to have strong and fast propagators for cumulative resource constraints. One such propagator is the recently developed time-table-edge-finding propagator, which considers the current resource profile during the edge-finding propagation. Recently, lazy clause generation solvers, i.e. constraint programming solvers incorporating nogood learning, have proved to be excellent at solving scheduling and cutting problems. For such solvers, concise and accurate explanations of the reasons for propagation are essential for strong nogood learning. In this paper, we develop the first explaining version of time-table-edge-finding propagation and show preliminary results on resource-constrained project scheduling problems from various standard benchmark suites. On the standard benchmark suite PSPLib, we were able to close one open instance and to improve the lower bound of about 60% of the remaining open instances. Moreover, 6 of those instances were closed.

Solving the Resource Constrained Project Scheduling Problem with Generalized Precedences by Lazy Clause Generation

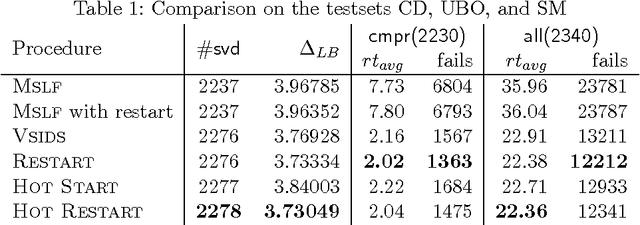
The technical report presents a generic exact solution approach for minimizing the project duration of the resource-constrained project scheduling problem with generalized precedences (Rcpsp/max). The approach uses lazy clause generation, i.e., a hybrid of finite domain and Boolean satisfiability solving, in order to apply nogood learning and conflict-driven search on the solution generation. Our experiments show the benefit of lazy clause generation for finding an optimal solutions and proving its optimality in comparison to other state-of-the-art exact and non-exact methods. The method is highly robust: it matched or bettered the best known results on all of the 2340 instances we examined except 3, according to the currently available data on the PSPLib. Of the 631 open instances in this set it closed 573 and improved the bounds of 51 of the remaining 58 instances.