Unsatisfiable Cores and Lower Bounding for Constraint Programming

Constraint Programming (CP) solvers typically tackle optimization problems by repeatedly finding solutions to a problem while placing tighter and tighter bounds on the solution cost. This approach is somewhat naive, especially for soft-constraint optimization problems in which the soft constraints are mostly satisfied. Unsatisfiable-core approaches to solving soft constraint problems in SAT (e.g. MAXSAT) force all soft constraints to be hard initially. When solving fails they return an unsatisfiable core, as a set of soft constraints that cannot hold simultaneously. These are reverted to soft and solving continues. Since lazy clause generation solvers can also return unsatisfiable cores we can adapt this approach to constraint programming. We adapt the original MAXSAT unsatisfiable core solving approach to be usable for constraint programming and define a number of extensions. Experimental results show that our methods are beneficial on a broad class of CP-optimization benchmarks involving soft constraints, cardinality or preferences.

Bigeometric Organization of Deep Nets

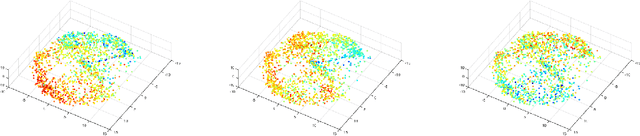
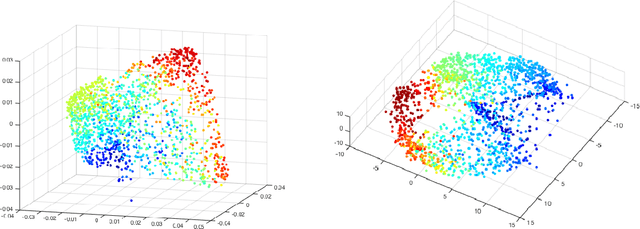
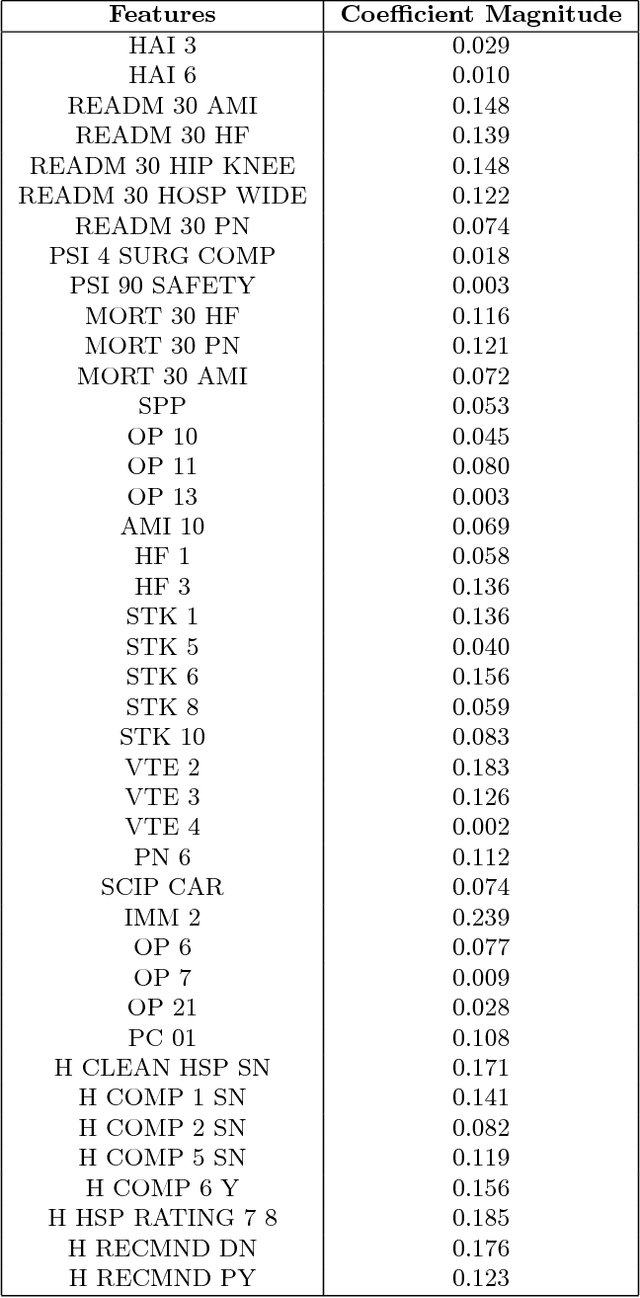
In this paper, we build an organization of high-dimensional datasets that cannot be cleanly embedded into a low-dimensional representation due to missing entries and a subset of the features being irrelevant to modeling functions of interest. Our algorithm begins by defining coarse neighborhoods of the points and defining an expected empirical function value on these neighborhoods. We then generate new non-linear features with deep net representations tuned to model the approximate function, and re-organize the geometry of the points with respect to the new representation. Finally, the points are locally z-scored to create an intrinsic geometric organization which is independent of the parameters of the deep net, a geometry designed to assure smoothness with respect to the empirical function. We examine this approach on data from the Center for Medicare and Medicaid Services Hospital Quality Initiative, and generate an intrinsic low-dimensional organization of the hospitals that is smooth with respect to an expert driven function of quality.

Unsatisfiable Cores for Constraint Programming

Constraint Programming (CP) solvers typically tackle optimization problems by repeatedly finding solutions to a problem while placing tighter and tighter bounds on the solution cost. This approach is somewhat naive, especially for soft-constraint optimization problems in which the soft constraints are mostly satisfied. Unsatisfiable-core approaches to solving soft constraint problems in Boolean Satisfiability (e.g. MAXSAT) force all soft constraints to hold initially. When solving fails they return an unsatisfiable core, as a set of soft constraints that cannot hold simultaneously. Using this information the problem is relaxed to allow certain soft constraint(s) to be violated and solving continues. Since Lazy Clause Generation (LCG) solvers can also return unsatisfiable cores we can adapt the MAXSAT unsatisfiable core approach to CP. We implement the original MAXSAT unsatisfiable core solving algorithms WPM1, MSU3 in a state-of-the-art LCG solver and show that there exist problems which benefit from this hybrid approach.