An Efficient Difference-of-Convex Solver for Privacy Funnel

We propose an efficient solver for the privacy funnel (PF) method, leveraging its difference-of-convex (DC) structure. The proposed DC separation results in a closed-form update equation, which allows straightforward application to both known and unknown distribution settings. For known distribution case, we prove the convergence (local stationary points) of the proposed non-greedy solver, and empirically show that it outperforms the state-of-the-art approaches in characterizing the privacy-utility trade-off. The insights of our DC approach apply to unknown distribution settings where labeled empirical samples are available instead. Leveraging the insights, our alternating minimization solver satisfies the fundamental Markov relation of PF in contrast to previous variational inference-based solvers. Empirically, we evaluate the proposed solver with MNIST and Fashion-MNIST datasets. Our results show that under a comparable reconstruction quality, an adversary suffers from higher prediction error from clustering our compressed codes than that with the compared methods. Most importantly, our solver is independent to private information in inference phase contrary to the baselines.

Efficient Alternating Minimization Solvers for Wyner Multi-View Unsupervised Learning

In this work, we adopt Wyner common information framework for unsupervised multi-view representation learning. Within this framework, we propose two novel formulations that enable the development of computational efficient solvers based on the alternating minimization principle. The first formulation, referred to as the {\em variational form}, enjoys a linearly growing complexity with the number of views and is based on a variational-inference tight surrogate bound coupled with a Lagrangian optimization objective function. The second formulation, i.e., the {\em representational form}, is shown to include known results as special cases. Here, we develop a tailored version from the alternating direction method of multipliers (ADMM) algorithm for solving the resulting non-convex optimization problem. In the two cases, the convergence of the proposed solvers is established in certain relevant regimes. Furthermore, our empirical results demonstrate the effectiveness of the proposed methods as compared with the state-of-the-art solvers. In a nutshell, the proposed solvers offer computational efficiency, theoretical convergence guarantees, scalable complexity with the number of views, and exceptional accuracy as compared with the state-of-the-art techniques. Our focus here is devoted to the discrete case and our results for continuous distributions are reported elsewhere.

The Wyner Variational Autoencoder for Unsupervised Multi-Layer Wireless Fingerprinting

Wireless fingerprinting refers to a device identification method leveraging hardware imperfections and wireless channel variations as signatures. Beyond physical layer characteristics, recent studies demonstrated that user behaviours could be identified through network traffic, e.g., packet length, without decryption of the payload. Inspired by these results, we propose a multi-layer fingerprinting framework that jointly considers the multi-layer signatures for improved identification performance. In contrast to previous works, by leveraging the recent multi-view machine learning paradigm, i.e., data with multiple forms, our method can cluster the device information shared among the multi-layer features without supervision. Our information-theoretic approach can be extended to supervised and semi-supervised settings with straightforward derivations. In solving the formulated problem, we obtain a tight surrogate bound using variational inference for efficient optimization. In extracting the shared device information, we develop an algorithm based on the Wyner common information method, enjoying reduced computation complexity as compared to existing approaches. The algorithm can be applied to data distributions belonging to the exponential family class. Empirically, we evaluate the algorithm in a synthetic dataset with real-world video traffic and simulated physical layer characteristics. Our empirical results show that the proposed method outperforms the state-of-the-art baselines in both supervised and unsupervised settings.

A Provably Convergent Information Bottleneck Solution via ADMM

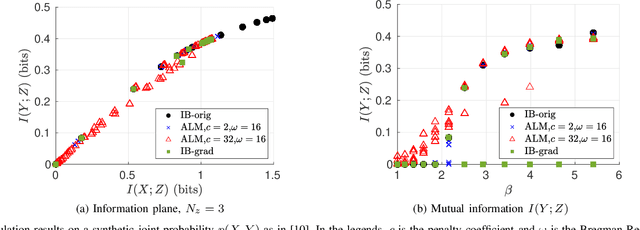
The Information bottleneck (IB) method enables optimizing over the trade-off between compression of data and prediction accuracy of learned representations, and has successfully and robustly been applied to both supervised and unsupervised representation learning problems. However, IB has several limitations. First, the IB problem is hard to optimize. The IB Lagrangian $\mathcal{L}_{IB}:=I(X;Z)-\beta I(Y;Z)$ is non-convex and existing solutions guarantee only local convergence. As a result, the obtained solutions depend on initialization. Second, the evaluation of a solution is also a challenging task. Conventionally, it resorts to characterizing the information plane, that is, plotting $I(Y;Z)$ versus $I(X;Z)$ for all solutions obtained from different initial points. Furthermore, the IB Lagrangian has phase transitions while varying the multiplier $\beta$. At phase transitions, both $I(X;Z)$ and $I(Y;Z)$ increase abruptly and the rate of convergence becomes significantly slow for existing solutions. Recent works with IB adopt variational surrogate bounds to the IB Lagrangian. Although allowing efficient optimization, how close are these surrogates to the IB Lagrangian is not clear. In this work, we solve the IB Lagrangian using augmented Lagrangian methods. With augmented variables, we show that the IB objective can be solved with the alternating direction method of multipliers (ADMM). Different from prior works, we prove that the proposed algorithm is consistently convergent, regardless of the value of $\beta$. Empirically, our gradient-descent-based method results in information plane points that are denser and comparable to those obtained through the conventional Blahut-Arimoto-based solvers.