Energy-Time Optimal Control of Wheeled Mobile Robots

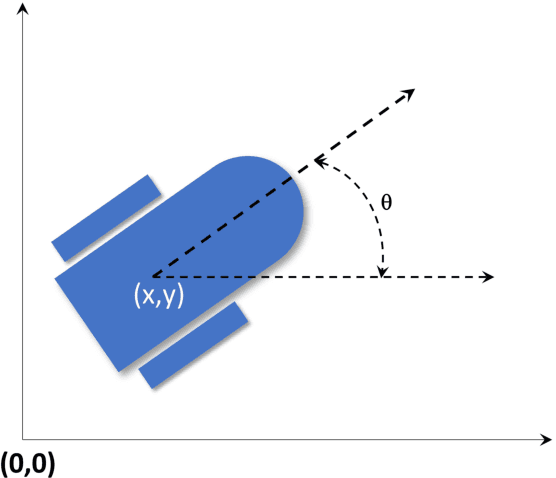
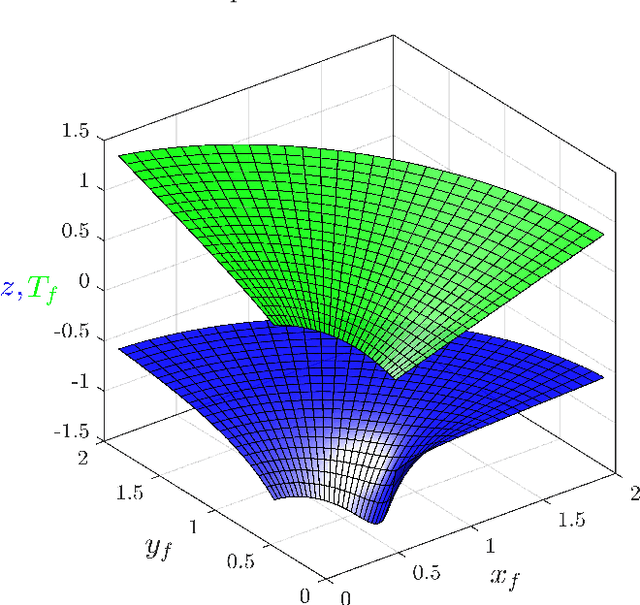
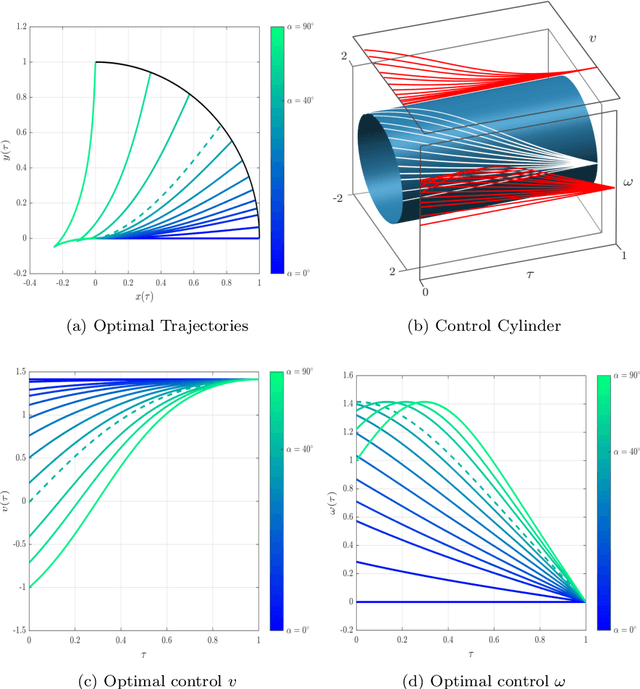
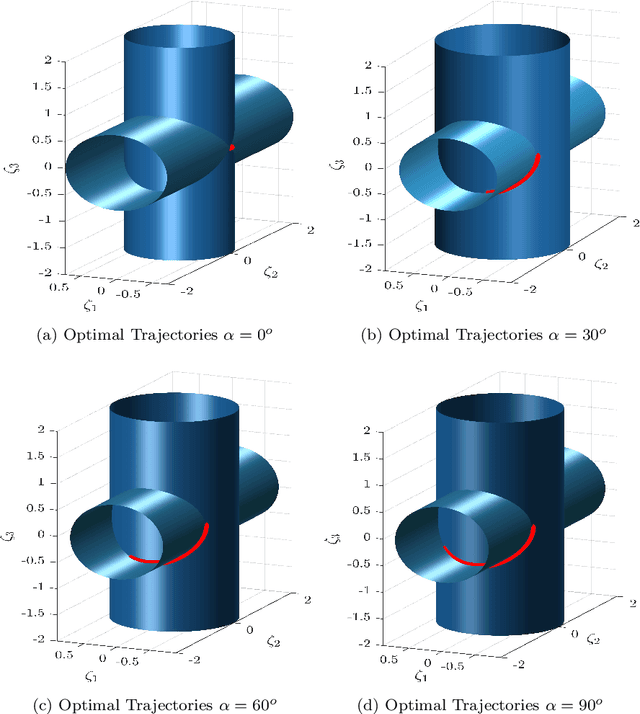
This paper focuses on the energy-time optimal control of wheeled mobile robots undergoing point-to-point transitions in an obstacles free space. Two interchangeable models are used to arrive at the necessary conditions for optimality. The first formulation exploits the Hamiltonian, while the second formulation considers the first variation of the augmented cost to derive the necessary conditions for optimality. Jacobi elliptic functions are shown to parameterize the closed form solutions for the states, control and costates. Analysis of the optimal control reveal that they are constrained to lie on a cylinder whose circular cross-section is a function of the weight penalizing the relative costs of time and energy. The evolving optimal costates for the second formulation are shown to lie on the intersection of two cylinders. The optimal control for the wheeled mobile robot undergoing point-to-point motion is also developed where the linear velocity is constrained to be time-invariant. It is shown that the costates are constrained to lie on the intersection of a cylinder and an extruded parabola. Numerical results for various point-to-point maneuvers are presented to illustrate the change in the structure of the optimal trajectories as a function of the relative location of the terminal and initial states.

Reduced-order modeling using Dynamic Mode Decomposition and Least Angle Regression

Dynamic Mode Decomposition (DMD) yields a linear, approximate model of a system's dynamics that is built from data. We seek to reduce the order of this model by identifying a reduced set of modes that best fit the output. We adopt a model selection algorithm from statistics and machine learning known as Least Angle Regression (LARS). We modify LARS to be complex-valued and utilize LARS to select DMD modes. We refer to the resulting algorithm as Least Angle Regression for Dynamic Mode Decomposition (LARS4DMD). Sparsity-Promoting Dynamic Mode Decomposition (DMDSP), a popular mode-selection algorithm, serves as a benchmark for comparison. Numerical results from a Poiseuille flow test problem show that LARS4DMD yields reduced-order models that have comparable performance to DMDSP. LARS4DMD has the added benefit that the regularization weighting parameter required for DMDSP is not needed.